# Understanding Why Negative Times Negative Equals Positive
Written on
Chapter 1: The Basics of Negative Numbers
The concept of multiplying a negative number by another negative number yielding a positive result is a fundamental principle taught to children in elementary school. Although it may seem straightforward, the question of why this is true often leaves many puzzled.
What is this puzzling question? It's simply:
Why does multiplying a negative number by another negative number yield a positive result?
In this discussion, we will delve into this question by examining core mathematical principles through a series of logical puzzles. This exploration will also reinforce your understanding of basic mathematical operations.
Section 1.1: The Role of Additive Identity in Addition
Addition is one of the most basic and instinctive mathematical operations. For instance, if a child has 2 candies in one hand and 3 in another, she might count them as she combines them into a new pile. This counting process reflects the act of addition, where she increases her total by one for each candy she counts.
Conversely, when she tries to divide the candies between herself and a friend, she counts backward. This act of counting down is what she will later recognize as subtraction. As children progress in their math education, they learn to perform these operations using abstract representations known as numbers.
When working with numbers, a crucial question arises:
What number, when added to or subtracted from another number, leaves that number unchanged?
The answer is zero (0), known as the additive identity. Now that we understand the additive identity, let's move on to a more complex topic.
Section 1.2: Understanding Subtraction vs. Negative Values
As children continue their mathematical journey, they learn that addition and subtraction can also involve negative numbers. For example:
3 + (-2) = 3 - 2 = 1
In this equation, adding a positive number (3) to a negative number (-2) results in the subtraction of the absolute value of the negative number from the positive number.
While this concept may seem simple, it hides a significant challenge: although subtraction is intuitive, negative numbers are not. The equation "3 - 2" can be easily understood as asking how many candies remain after giving some away. However, the notion of -2 candies is less clear. While we might say the child owes 2 candies, this meaning is contextually assigned.
Essentially, negative numbers are abstract concepts that require contextual meaning. They are not derived from everyday experiences in the same way that positive numbers are. The key takeaway here is:
Adding a negative number to a positive number results in a subtraction operation where the absolute value of the negative number is deducted from the positive number.
We now have a framework for handling both positive and negative numbers in addition. Let’s further extend this to subtraction.
Chapter 2: Subtracting Negative Values
When subtracting a negative number from a positive one, the operation transforms into addition where the absolute value of the negative number is added to the positive one. For example:
3 - (-2) = 3 + 2 = 5
Furthermore, subtracting one negative number from another leads to addition, which simplifies to a situation where a positive number is combined with a negative number:
-2 - (-2) = -2 + 2 = 0
This example highlights an essential point:
A negative number (-x) is defined as one that, when added to its positive equivalent (x), results in the additive identity (zero).
Now, let’s transition to multiplication.
Section 2.1: Multiplication and Its Identity
Multiplication, while a more advanced operation, can still be understood intuitively as repeated addition. For instance:
2 * 3 = 3 * 2 = 6
The left side of this equation asks: What is the total when we add two, three times? The middle part asks: What is the total when we add three, two times? Both yield the same result, illustrating the property of commutativity — the order of factors does not affect the product.
Next, we ponder:
What number, when multiplied by a given number, keeps that number unchanged?
The answer is one (1) — the multiplicative identity. Any number multiplied by 1 remains unchanged. With this concept established, we can explore the multiplication of negative numbers.
Section 2.2: Multiplying Negative Numbers
It's evident that multiplying two positive numbers results in a positive number (e.g., 2 * 8 = 16). But what occurs when a positive number is multiplied by a negative number? Consider:
2 * (-8) = ?
This can be interpreted as asking what happens when we add two, (-8) times:
2 * (-8) = (-8) + (-8) = -16
Thus, we see that multiplying a positive number by a negative number results in a negative number:
(+) * (-) = (-)
Now we are prepared to address our original question:
Chapter 3: The Answer to Why Negative Times Negative Equals Positive
We already established that ‘1’ is the multiplicative identity. Multiplying any number by ‘1’ yields the original number. So, what about ‘-1’? It represents the opposite of the multiplicative identity, reversing the sign of any non-zero number it multiplies. For example:
- (-1) * (1) = -1
- (-1) * (25) = -25
- (-1) * (a) = -a
Using this logic, we can deduce that ‘(-1) * (-a) = +a’. However, this reasoning may not be entirely convincing. Instead, let’s explore a different approach.
Imagine a scenario where the expression ‘(-1) * (-1)’ is unknown. We start with the equation:
1 + (-1) = 0
Next, we multiply both sides by ‘-1’ and apply the distributive law:
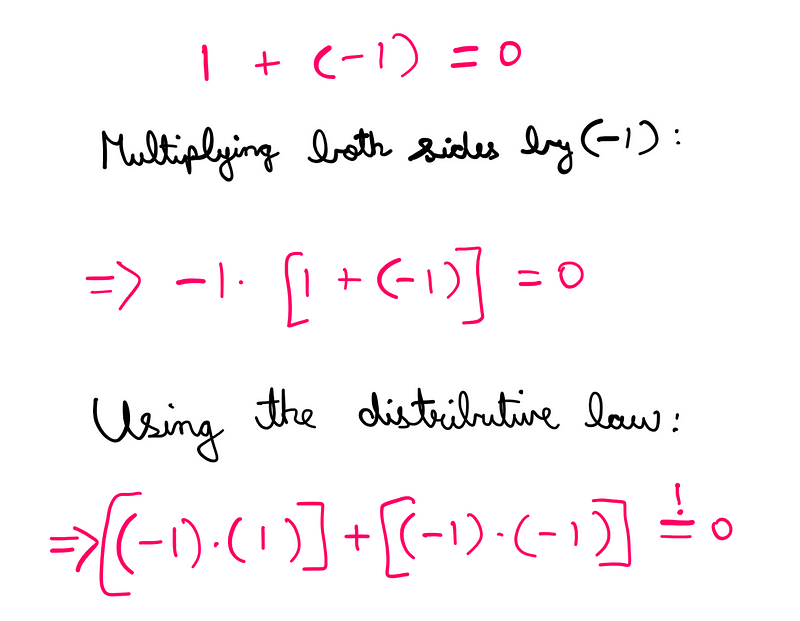
The left side represents what we’ve seen: any number multiplied by ‘-1’ reverses its sign, resulting in ‘-1’. The second part, however, is what we seek to discover.
Since we don't know the value of ‘(-1) * (-1)’, we designate it as an unknown (x). This leads us to:

Thus, we arrive at:
(-1) * (-1) = +1
Generalizing this result gives us:
(-) * (-) = (+)
Final Thoughts
In summary, we have shown why multiplying two negative numbers results in a positive number by following a logical progression through fundamental mathematical operations.
- We began with addition and subtraction, focusing on the additive identity (0).
- We distinguished the difference between subtraction and negative numbers.
- We explored addition and subtraction involving negative numbers.
- We discussed multiplication and the multiplicative identity (1).
- We established that (+) * (-) = (-).
- Finally, we demonstrated that multiplying two negative numbers leads us back to a positive value.
The reason why negative times negative equals positive is that our mathematical framework necessitates this outcome to maintain logical consistency. As we build upon our understanding of core mathematical operations, this truth naturally emerges.
For further reading, consider exploring topics such as "Why Exactly Is Zero Factorial Equal To One?" and "Why Is A Number Raised To The Power Zero = One?"
If you would like to support my work as an author, consider contributing on Patreon.