Understanding Irrational Exponents: A Deep Dive
Written on
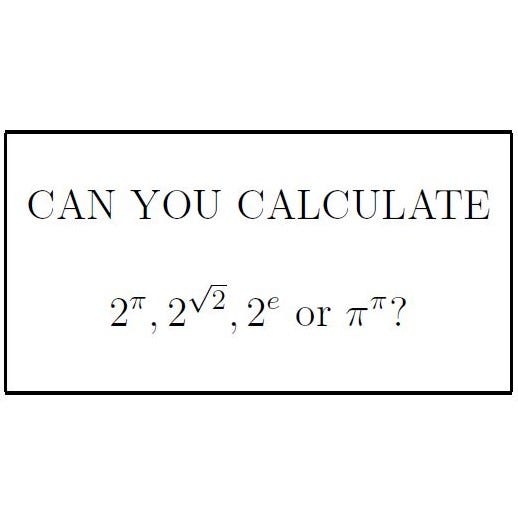
Have you ever pondered how to compute an irrational exponent? For instance, consider the value of

While you might deduce that ? is slightly greater than 3, you could guess that
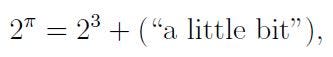
and your estimation would be relatively accurate. Indeed, it turns out that
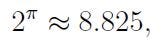
and it likely won’t surprise you that it is classified as an irrational number. But how do we arrive at this conclusion? Typically, we are taught that a number such as
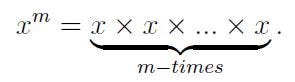
However, this definition primarily applies when m is a positive integer. For example, asserting
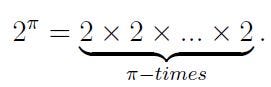
creates ambiguity. In this discussion, we will delve into a precise definition of exponents and analyze how calculators or computing software typically processes these computations.
Initially, let’s focus on the values of
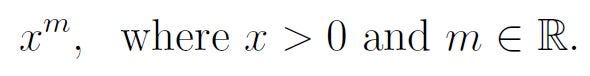
We will address the implications of x < 0 towards the end of our discussion.
As previously mentioned, when m is a positive integer, the commonly accepted definition is that
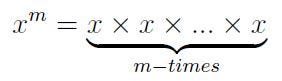
This definition holds true, even if we consider m to be a negative integer. By applying the exponent rule
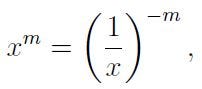
and substituting n = -m > 0, we find that

However, this definition begins to fail when we introduce rational numbers. Specifically, defining
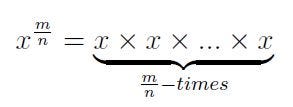
is problematic. Nevertheless, we can salvage it by recalling an addition rule for exponents. For n ? 0,
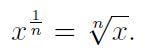
This allows us to reinterpret the definition as
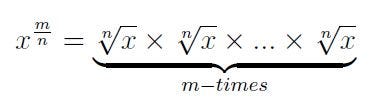
and thus our definition is valid again.
Once we permit m to be irrational, the original definition collapses. It is illogical to multiply an irrational number, like ? or e, a specified number of times.
The best approach with this initial definition is to provide an approximate interpretation. For example, if we set x = 2 and m = ? We can approximate ?, to any desired precision, through methods like Taylor’s theorem. This allows us to assert that
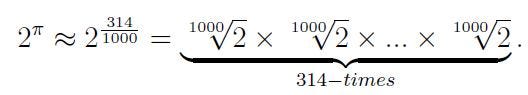
Alternatively, employing the well-known approximation of
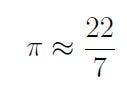
yields a similar result
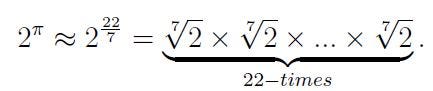
While this method is functional, it lacks elegance and, more importantly, does not constitute an accurate definition. However, it is possible to derive a valid definition from this approach. The greater the accuracy of our approximations, the closer the interpretation aligns with accuracy.
Consequently, if we examine a sequence of approximations for our number, such as

we might propose that

An alternative representation is to let
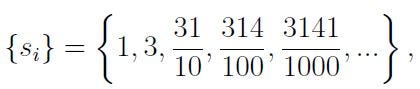
which denotes the sequence of approximations to ?, and we can propose that

It seems that this definition holds and is intuitively sound. The main issue, however, is that throughout this discussion, we have assumed that the limit of these sequences is valid! If not, we revert to an absurd definition.
Thus, for x > 0 and m irrational, to establish a definition such as
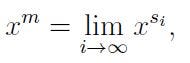
where {s_i} is the sequence of approximations to m, we must ensure the limit exists. This requirement could be straightforward, but we face a second challenge: How do we determine which sequence of approximations to utilize? For instance, we defined

but we could have equally defined it through
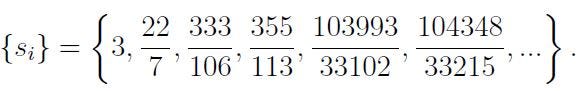
If you are unfamiliar with this sequence, it originates from the continued fraction approximations of ?, and I assure you that these terms converge to ?.
Thus, for our definition to be effective, we must demonstrate that
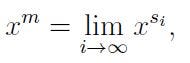
holds true regardless of our choice of “sequences of approximations” {s_i}, which can be quite an undertaking. In summary, although this definition is intuitively appealing, it can be quite complex to apply.
What Definition Do Mathematicians Use?
I’m glad you asked! For x > 0, we define
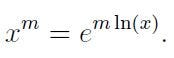
I can anticipate your thoughts: this seems more intricate than our original definition. Let’s deconstruct it to understand why it works and why this definition is indeed easier to compute. There are various definitions for both the exponential function and the natural logarithm function. We will examine two specific definitions, and don’t fret if these are unfamiliar to you.

This definition of the exponential function arises from Taylor’s theorem, while the natural logarithm function is derived from university calculus courses. As previously mentioned, don't be concerned if these concepts are new to you; the crucial takeaway is that they can be computed relatively easily and, importantly, unlike the earlier definition, they are both well-defined, eliminating discrepancies in results.
Regarding our definition, it is simply a manipulation stemming from the fact that the exponential and natural logarithm functions are inverses, i.e.,
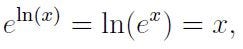
and the logarithmic rule
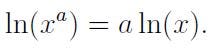
Specifically,
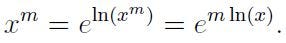
As a concrete example, we now observe that

Two noteworthy points emerge: 1. As you can see, programming a calculator to compute, or at least approximate, values that involve irrational exponents is significantly simpler using this definition compared to our prior definition. To my knowledge, this is precisely how your calculator or software computes such values. 2. This definition not only aligns with our earlier definition for rational m but also confirms that all the exponent rules we know still apply. For instance, we see that
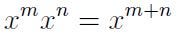
still holds true since
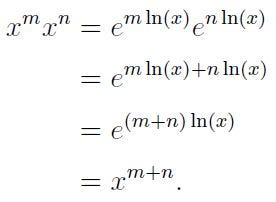
I encourage you to verify other exponent rules such as
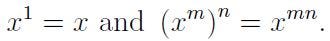
Thus, provided x > 0, we adopt the definition
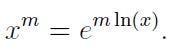
What About x < 0?
Great question! We certainly cannot utilize the preceding definition, as it would necessitate evaluating
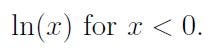
Or can we? This matter is slightly more intricate—not because our definition fails, as it still holds when we introduce complex numbers and principal branches. If you're unfamiliar or uneasy with these concepts, don’t worry; I won't delve too deeply into this article as it requires more extensive discussion. However, I will provide a brief overview of what occurs.
In a simplified and somewhat imprecise explanation, it’s crucial to know that in the complex plane, certain functions, such as ln(x), become “multi-valued.” This indicates that, unlike in the real plane, ln(x) can assume multiple values in the complex realm.
As an analogy, consider the inverse sine function. We know that
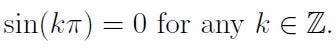
This illustrates that the inverse sine function is multi-valued, as we must have

Given that
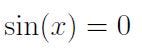
it’s impossible to determine the precise value of x without first limiting the inverse sine function. For instance, if we restrict our focus to the range [?, 2?), we can confidently state that

When dealing with multi-valued functions like ln(x) in the complex plane, we approach the situation similarly. This restriction is known as selecting a branch of ln(x), typically opting for a specific restriction termed the principal branch of ln(x). I’m being somewhat vague on the specifics here, as they are not necessary for this article, but if you wish for me to elaborate on this topic in a future article, just let me know. The crucial point is that this approach allows us to navigate challenges associated with calculating ln(x) when x < 0 and retains the integrity of our definition.
In conclusion, with a few adjustments, we can define, for all x, m ? ?,
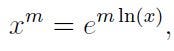
where ln(x) denotes a specific branch of the natural logarithm function in the complex plane. The key takeaway is that, while many calculators may yield different results,
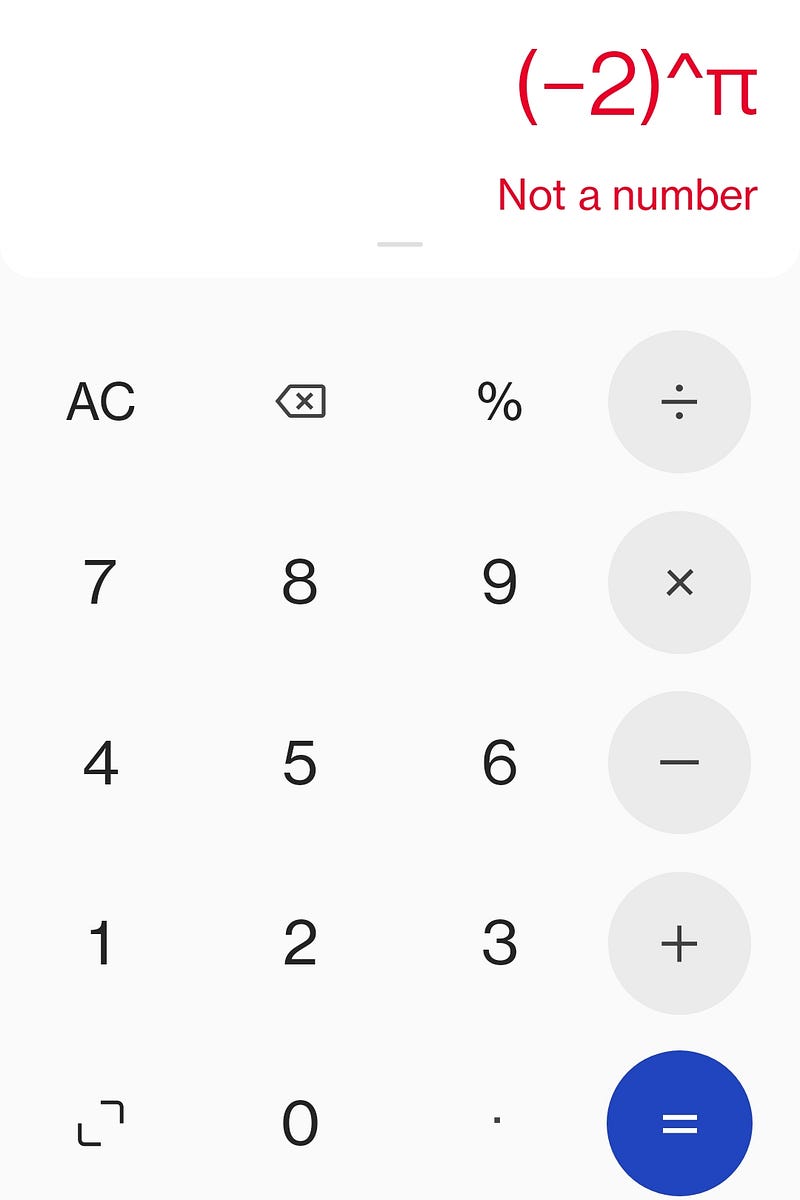
we can determine

Although if m is irrational and x < 0, then
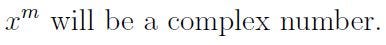
I hope you found this article as enjoyable to read as I did to write. I cherish questions like this that prompt me to reconsider my understanding of foundational mathematical principles I employ daily. These are often concepts that I, and likely many of you, take for granted without a second thought. However, upon deeper reflection, they reveal a much richer landscape than we initially perceive, adding to the intrigue.
Thank you for taking the time to read.
I would be grateful if you would consider following me and my publication Y(Math) to extend the reach of my articles.
Additionally, if you are interested in contributing to Y(Math), please feel free to submit an article draft to [email protected]. We would love to welcome more writers!