Chapter 1: Revisiting Basic Geometry

While assisting my seventh-grade daughter with her math homework, I found myself reflecting on a fundamental principle in plane geometry: the total of the exterior angles in a convex polygon is always 360 degrees. This brought back memories of my own middle school education, where we learned that the sum of the angles in a triangle is 180 degrees. By dividing an n-sided convex polygon into (n-2) triangles, we can determine that the total interior angles of the polygon equal (n-2)×180 degrees. Since an interior angle and its corresponding exterior angle add up to 180 degrees, it follows that the total of all exterior angles is simply:

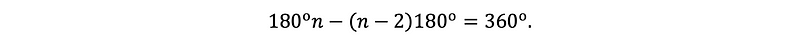
The reasoning behind this mathematical fact left me questioning whether I was ever truly captivated by it in my own schooling. Often, students are merely required to memorize mathematical facts to solve straightforward problems without delving deeper into the concepts. Yet, this simple result is remarkable as it holds true regardless of the number of sides in the polygon. I find the standard textbook proof somewhat unfulfilling, as the variable n seems to vanish without any clear rationale.

To make this concept more relatable for a middle schooler, we can visualize walking along the edges of the polygon while holding a rod extended in front. As we walk forward, the rod maintains its direction. It only sweeps at an angle when we transition from one side to another. Therefore, irrespective of how many sides the polygon has, the total of the exterior angles corresponds to the cumulative angles swept by the rod upon returning to the starting point. Even my daughter could grasp that the answer is consistently 360 degrees.

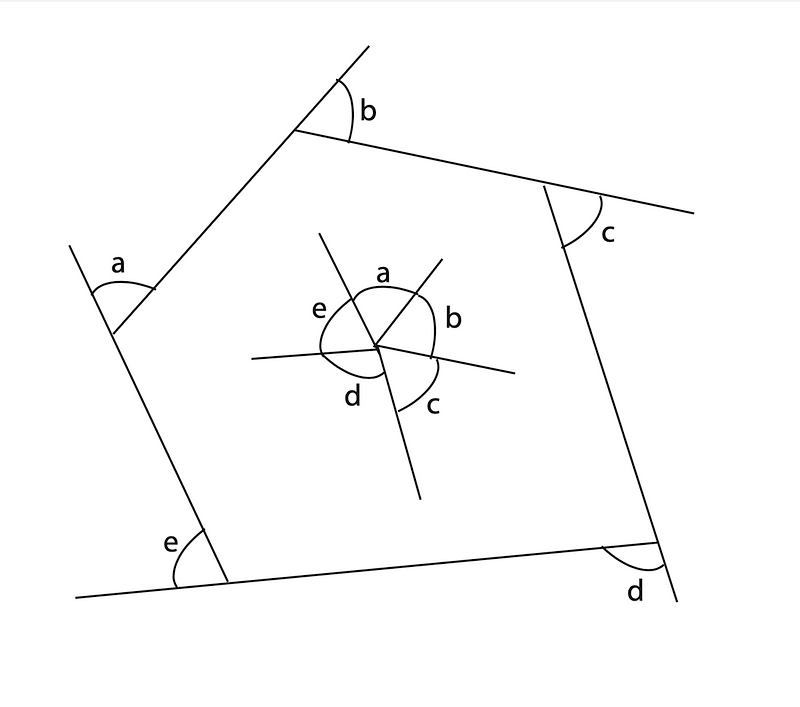
To establish a more rigorous foundation, we can consider that the size of the polygon is irrelevant. If we scale the polygon by a factor of r, as r approaches zero, we create an infinitesimal polygon maintaining the same orientation (see the inner polygon). By correlating the corresponding angles of parallel lines, it becomes evident that the exterior angles form around a point, leading to a total of 360 degrees.

This intuitive approach can be easily extended to concave polygons. As we traverse the sides of a concave polygon, the rod may sometimes sweep in the opposite direction. Regardless of how unconventional the concave polygon may appear, the total angle swept by the rod remains 360 degrees when we return to our starting position, provided we define angles swept in the opposite direction as negative. This presents an excellent opportunity to introduce a middle schooler to the concept of negative numbers. Just as we can use opposite signs to denote forward and backward movement, we can also represent rotations in clockwise and counterclockwise directions similarly.

It’s easy to envision that this result applies to any closed loop. While a high school calculus approach can readily prove it for circles, demonstrating the general case might require more advanced tools. The straightforward geometric fact my daughter is studying in middle school is, in fact, a topological concept. If approached or taught correctly, this elementary principle can have far-reaching implications.

Chapter 2: Engaging with Mathematical Concepts

No youtube to insert. Don't generate youtube directive.