Mastering Percentage Calculations with Negative Values
Written on
Chapter 1 Understanding Percentages with Negative Values
Calculating percentages involving negative numbers can be more complex than one might think.
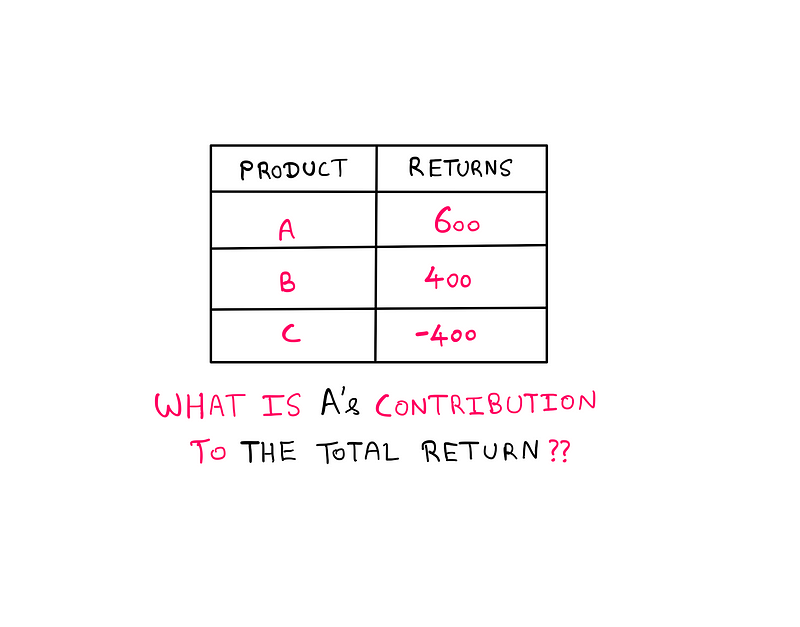
Image created by the author
When is it essential to consider percentages with negative values? The common response might be "rarely, if ever!" However, this scenario arises more frequently than most assume. Often, these calculations are performed behind the scenes, leaving users unaware of their implications. If we don’t grasp the calculations we are utilizing, we risk making ill-informed decisions in significant contexts.
Before delving deeper, let’s clarify what we mean by percentages with negative values.
Section 1.1 Defining Percentages with Negative Values
Typically, we associate percentage calculations with positive numbers. A percentage expresses a portion of a whole. For instance, if a theater has 750 filled seats out of 1200, we calculate it as (750/1200)*100 = 62.5% filled. Consequently, 37.5% of the seats remain unoccupied. This simple percentage provides a clear view of the situation, allowing us to focus on:
- The proportion of the theater that is filled.
- The proportion that is still available.
So far, so straightforward. Now, imagine a scenario in which you run a business offering three products: A, B, and C. At the end of the first month, the returns for each product line appear as follows:
Product Returns Table — created by the author
Product A has generated 600 monetary units, Product B 400, and Product C has resulted in a loss of 400 monetary units. Your challenge now is to determine the percentage contribution of each product to the total business performance at month’s end.
This hypothetical situation reflects a common occurrence in various contexts, highlighting that this is not merely a theoretical problem.
Section 1.2 Standard Method for Calculating Percentages
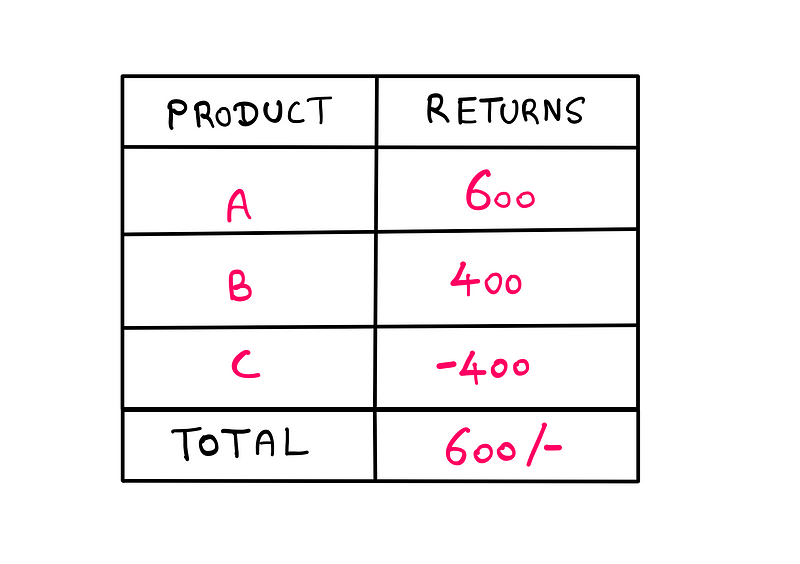
Let’s begin with the conventional approach to calculating percentages. First, we would compute the total revenue, which in this case is 600 monetary units. To find the percentage contribution of Product A, we would divide its return by the total return and multiply by 100:
(600/600)*100 = 100%
However, this seems incorrect. It’s implausible that Product A alone accounts for 100% of the total return when Product B is also profitable and Product C is not. If we sum the contributions of Products A and B, we would exceed 100%. What’s going wrong, and how should we adjust our calculations?
Renowned mathematician Jordon Ellenberg advises:
“Don’t talk about percentages of numbers when the numbers might be negative.”
While I appreciate this wisdom, reality often demands a specific percentage. If a client or investor requests this information, I cannot simply dismiss their request. So how do we navigate this?
Chapter 2 Adjusting Calculations for Clarity
The core of the challenge lies in the question we are asking:
What percentage has each product contributed to the bottom line of the business at the end of the month?
When negative numbers are involved, this question is insufficient. We need to clarify what type of percentage we are calculating. This leads to additional inquiries:
- Why is it essential to know each product's percentage contribution?
- Is it beneficial to distinguish between profitable and non-profitable products?
Suppose an investor wants to identify which products are successful and which are not. In this case, calculating percentages based on absolute values makes sense. The calculations would appear as follows:
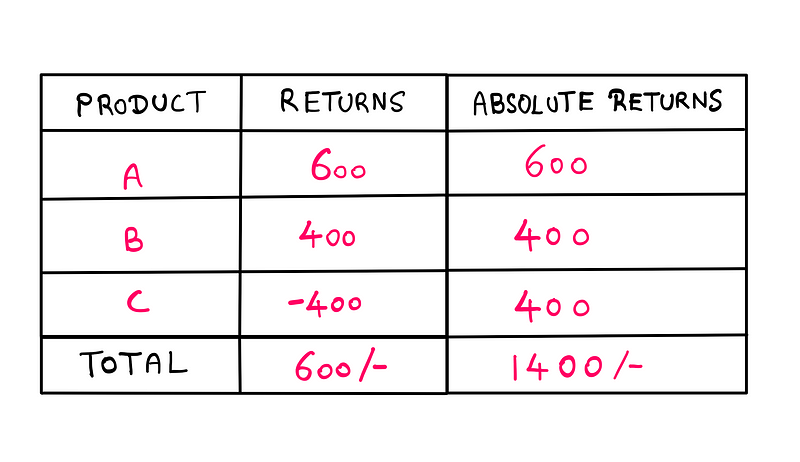
Product Returns Table with Absolute Returns — created by the author
Now, we can determine the percentage contributions of each product to the total absolute revenue:
- Product A: (600/1400)*100 = 42.86%
- Product B: (400/1400)*100 = 28.57%
- Product C: (400/1400)*100 = 28.57%
You may question how Product C can contribute 28.57% when it reflects a loss. This brings us back to our earlier question regarding the differentiation of profitable from non-profitable products.
Section 2.1 Contextualizing Percentage Calculations
When discussing terms like "revenue" or "profit," we typically expect positive figures, which can skew our interpretations. Instead, we could redefine the net absolute revenue as “net change” and separate profitable from non-profitable contributions. This report would look as follows:
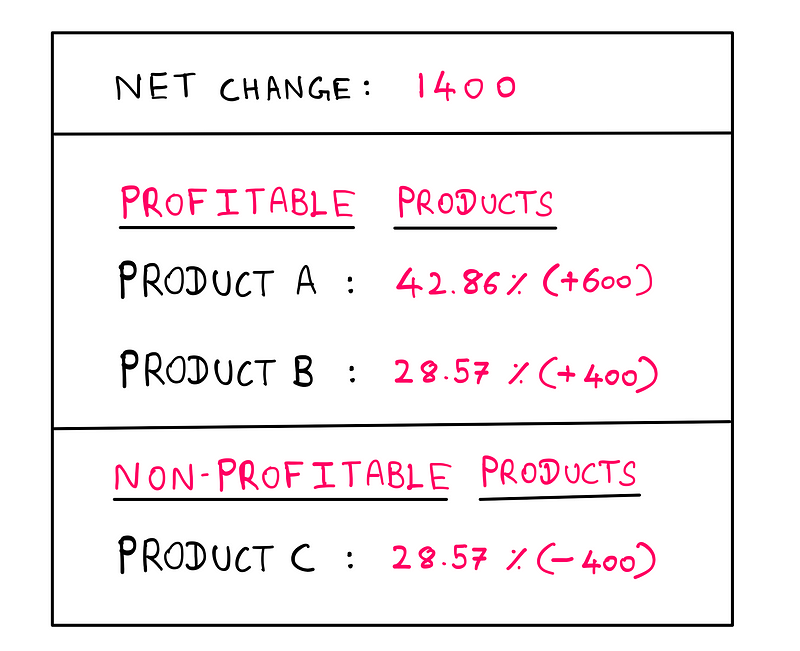
Product Percentage Contribution Report — created by the author
This structure allows us to see each product's contribution to the overall performance while retaining clarity about which products are thriving and which are not.
Section 2.2 Real-World Applications
The example provided illustrates a broader need for calculating percentages involving negative numbers. Such issues arise frequently in fields like bookkeeping and operations research. You might believe you’re exempt unless you work directly in these sectors, but consider this: if you’re an end-user of information produced by these calculations, you must be vigilant about what you’re interpreting.
As we have demonstrated, different calculation methods can yield varied interpretations. There’s no absolute right or wrong; it all hinges on the purpose behind the numbers generated.
In summary, when faced with negative values, approach percentage calculations with skepticism and curiosity. Assess what information is most relevant for your decision-making and whether it can be derived from the existing data. If you are generating these figures, strive to provide multiple calculation methods tailored to different scenarios and users.
To wrap up, exercise caution when calculating percentages with negative numbers and evaluate the results diligently!
The first video titled "Calculating Percentage Change When The Base Value Is Negative" delves into how to effectively handle such calculations in various contexts.
The second video, "How to Convert Negative Percentages: Easy-to-Intermediate Math," offers a straightforward approach to understanding and converting negative percentages.
Further reading that might interest you: How To Really Deal With The Friendship Paradox? and What Is So Special About 69! ?
If you would like to support me as an author, consider contributing on Patreon.