Exploring the Fair-Square Game: Origins of Geometric Probability
Written on
Chapter 1: Introduction to the Franc-Carreau Game
The Franc-Carreau, also known as the fair-square game, is a chance-based game that emerged during a time when the mathematical concept of probability was just beginning to influence the gambling world. In the 18th century, Georges-Louis LeClerc, Comte de Buffon, was eager to join the Royal Academy of Sciences in Paris. Despite holding a law degree, Buffon's passion for science led him to abandon a legal career in favor of mathematics after encountering Swiss mathematician Gabriel Cramer.
To pursue his ambition, Buffon authored a groundbreaking paper that bridged geometry and probability—two fields previously viewed as unrelated. He initiated this work by designing the simple game of Franc-Carreau, which raises intriguing questions about the intersection of geometry and chance.
Section 1.1: The Mechanics of the Game
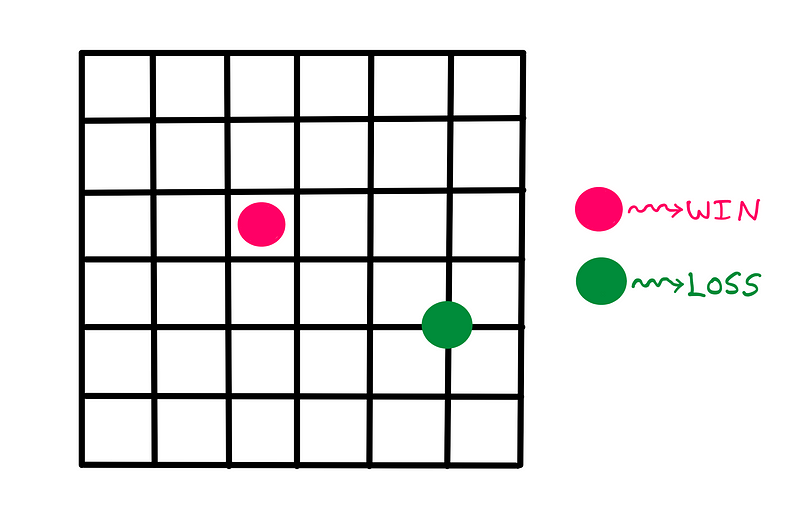
The term "Franc-Carreau" translates roughly to "tile within a tile" or "square within a square." The game employs a coin (historically, an ecu was used) and a square grid or board. Players toss the coin onto the grid, winning if it lands entirely within a square. Conversely, touching any grid lines results in a loss.
To illustrate, consider the example below where a pink coin lands wholly within a square, while a green coin touches multiple grid lines.
Section 1.2: Buffon's Geometric Approach
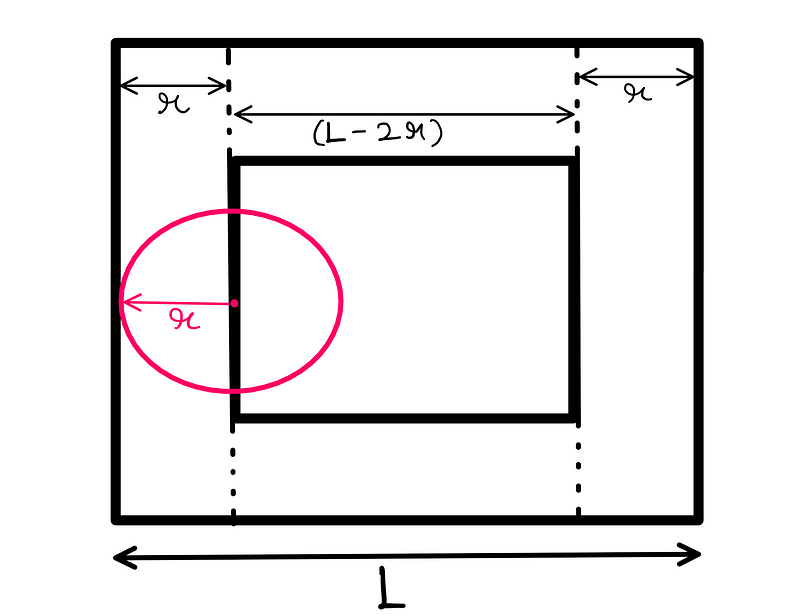
Buffon sought to determine the necessary dimensions of the coin and grid to ensure the Franc-Carreau game was fair, providing a 50% chance of winning. He envisioned a smaller square positioned within a larger square, equidistant from each edge of the larger square. Let’s denote the length of each grid square as ‘L’.
If a circular coin with radius ‘r’ lands such that its center aligns with one edge of the smaller square (of length (L-2r)), it will just touch that edge. The illustration below provides a visual representation:
Subsection 1.2.1: The Probability Calculation
Buffon then aimed to calculate the probability of the coin landing within the smaller square based on area ratios. The probability that the coin lands completely inside the smaller square can be expressed as:
P = frac{(L-2r)²}{L²}
To create a fair game, this probability must equal ½. Thus, the equation becomes:
frac{(L-2r)²}{L²} = frac{1}{2}
This simplifies into a quadratic equation, leading to:
L = (4 + 2sqrt{2})r
Through this relationship, Buffon demonstrated that the Franc-Carreau game could maintain a fair 50% winning chance.
Chapter 2: Buffon’s Legacy in Probability
In the first video, "How to make a custom board game Pt.1," viewers are guided through the process of creating a personalized board game, exploring the foundational concepts of game design.
The second video, "Level Design with Gamefroot," delves into the intricacies of level design, showcasing tools and techniques for crafting engaging game environments.
Final Thoughts
While the Franc-Carreau game appears simple, Buffon's work is regarded as a pivotal moment in the development of geometric probability. This was merely the beginning for Buffon, who would later tackle more complex geometric probability challenges, which I plan to explore in a forthcoming essay.
For further reading, consider topics such as "How To Really Benefit From Curves Of Constant Width?" and "How To Benefit From Braess’s Paradox?" If you appreciate my work, feel free to support me on Patreon.