Understanding the Distinction Between a Donut and a Sphere
Written on
Chapter 1: Introduction to Homotopy Groups
In this section, we will explore how functions can be transformed from one form to another using the concept of homotopy. Consider two spaces, X and Y. If these spaces are homotopy equivalent, it implies that their corresponding homotopy groups are identical.
One method to differentiate a donut from a sphere is by analyzing the types of loops that can be drawn on their surfaces. You can easily convince yourself that a loop drawn on a sphere's surface can be shrunk down to a single point without difficulty. In contrast, the situation is different for a donut. While it's possible to create a small loop that can be contracted to a point, there are certain loops—like the one illustrated to the right—that cannot be reduced in this manner. In the following sections, we will delve deeper into these mathematical principles.
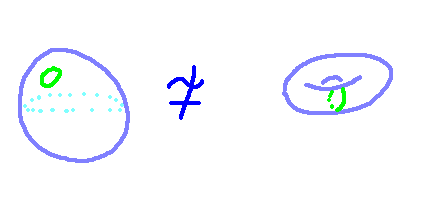
Homotopy Groups Explained
The homotopy group of a space provides insight into the mathematical framework of closed loops that can be drawn within that space. Specifically, the homotopy group at a particular point consists of equivalence classes of closed paths that are homotopic to one another. But what exactly is homotopy? Two functions are considered homotopic if one can be smoothly transformed into the other. Since paths can be viewed as functions, the same principle applies to paths. A path within a space can be described as a mapping from the interval [0, 1] to the space, where the distance along the path is assigned a specific value.
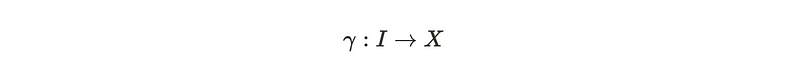
For two paths to be considered homotopic, a continuous map F must exist that smoothly deforms one path into another within the space. In the equation that follows, when the map F takes the value 0 as its first argument, it corresponds to path 1, which is denoted by the function gamma_1.
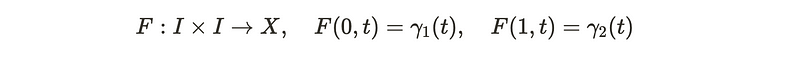
The group operation between equivalence classes of homotopic paths is not immediately clear and will be addressed in a future discussion.
Homotopic Spaces and Their Properties
Let's consider two topological spaces, X and Y. Just as we can map paths between them using a function f, a function that moves from Y to X with a composition that is homotopic to the identity map indicates that these two spaces are homotopy equivalent. A classic example of this scenario is a single point in relation to the real space R³. Spaces that can be homotopically reduced to a point are referred to as contractible.

If two spaces are homotopy equivalent, what can we infer about their homotopy groups? As anticipated, homotopy equivalent spaces possess isomorphic structure groups. Although the reasoning behind this may not be immediately apparent, it can be proven. This isomorphism arises from the star map of the equivalence function, and demonstrating its bijection is crucial—signifying that if a space is homotopy equivalent to a circle, its homotopy group corresponds to Z.
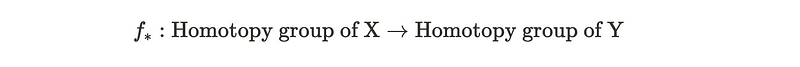
Mathematically, the homotopy group of a space X at a base point x_0 is denoted as follows:
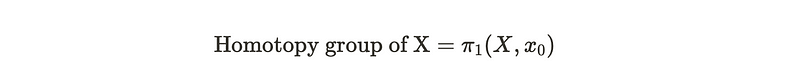
Proof of Homotopy Group Functionality
When we have a function mapping from space X to space Y, we can establish a connection between the equivalence classes of loops, thereby creating a function between the homotopy groups. The objective is to demonstrate that this function is well-defined, that it serves as a homomorphism between groups, and to investigate how to extend this map to the homotopy groups.
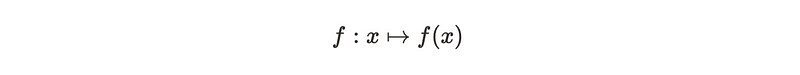
A member of the homotopy group in X is represented as [gamma]. The induced map transforms this into the composition of the path with the function itself. This prompts an important consideration: is this mapping well-defined?
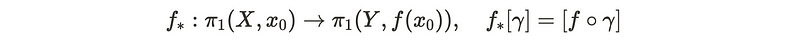
To verify its well-defined nature, we need to ensure that two paths within the same homotopy class lead to the same result. In simpler terms, if we have two homotopic paths, their images must also be homotopic. This can be easily confirmed by composing the original homotopy between the paths.
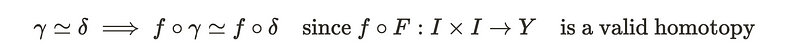
The demonstration of f_* being bijective is somewhat indirect; we utilize the following commutative diagram to clarify the process.
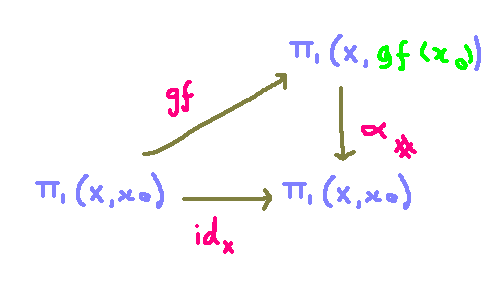
Through this identity, we can observe that since the hash map on alpha is an isomorphism, f_* must be injective. By applying this reasoning in reverse from space Y, we conclude that f must be surjective, confirming that the hash map functions as an isomorphism.
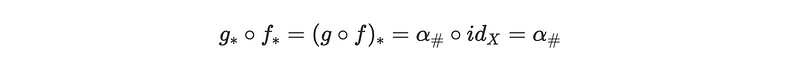
Chapter 2: Visualizing the Concepts
In the video "A donut is not a sphere | Things you can do on one surface but not the other," the differences between a donut and a sphere are visually demonstrated. The video elaborates on how certain topological properties distinguish these two shapes.
Additionally, "163: How to SHAPE Doughnuts 3 WAYS - Bake with Jack" provides a unique perspective on the physical attributes of donuts, further illustrating the contrast between these two geometric forms.