The Enigmatic Attraction of Simplicity in Science
Written on
Chapter 1: The Allure of Simplicity
Given the intricate tapestry of our universe, one might wonder: why is simplicity so cherished in science? As the English mathematician and philosopher Alfred North Whitehead articulated, the fundamental goal of science is to uncover the simplest explanations for complex phenomena. This insight resonates deeply with my own writing aspirations. However, this pursuit of simplicity quickly becomes complicated. What do we truly mean by "simplicity"? Does it align with what others perceive?
This quest isn't ours alone; every scientist and mathematician shares a common drive for simplicity in their theories and laws. If asked, could they provide an objective definition of simplicity? And if they could, would it be quantifiable? Assuming we could measure simplicity, what advantages would this bring to our scientific methods? If these questions pique your curiosity, I invite you to join me as we delve into the concept of simplicity within the realm of science.
Section 1.1: A Historical Perspective on Simplicity
In the 17th century, German polymath Johannes Kepler staunchly defended his initial idea that planetary orbits must be circular, viewing the circle as the most straightforward closed curve. Ultimately, he recognized that orbits were elliptical, a conclusion he derided as "dung" that he had to accept to eliminate greater misunderstandings in astronomy. Kepler longed for an elegantly simple scientific model.
As time progressed, scientific discoveries unveiled even more intricate models, yet the appeal of simplicity persisted. Isaac Newton eloquently remarked, “Nature finds joy in simplicity and does not favor unnecessary complexities.” Although Newton’s laws were more complex than Galileo’s, they still maintained a degree of simplicity until Albert Einstein introduced even more intricate equations. Einstein believed, “Our experiences lead us to trust that nature embodies the simplest conceivable mathematical concepts.” In his work on gravitation, he opted for the simplest set of tensor equations to describe the phenomenon, stating to mathematician John G. Kemeny, “God would not miss the chance to render nature that simple.”
Thus, history reveals a consistent admiration for simplicity in science, despite the absence of an objective definition. What is the current status of simplicity in the scientific landscape?
Section 1.2: Simplicity in Contemporary Science
Imagine a data scientist aiming to establish a functional relationship between two variables. She plots her observations on a graph:
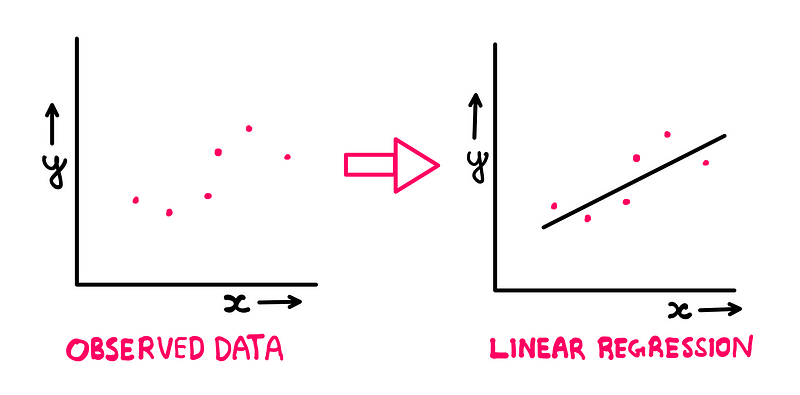
It's intriguing that the data scientist will likely seek to connect these points with the simplest curve possible. If the observations appear close to a straight line, she might assume her data is slightly flawed and choose to draw a straight line that misses all points. If this line fails to predict future observations accurately, she would consider a more complex curve. This preference for simplicity arises because simpler models generally have a higher likelihood of accurately describing phenomena.
Many natural laws are surprisingly straightforward. For example, nature often seeks extrema, aiming for points where the derivative of a function equals zero. This raises an essential question: Is nature inherently simple?
Section 1.3: The Complexity of Natural Simplicity
We must tread cautiously when considering simplicity in nature. It does not necessarily mean that nature favors simplicity; rather, it is our human inclination that drives us to seek it. Whitehead cautioned that we may mistakenly assume nature is fundamentally simple due to our quest for simplicity.
Take Einstein's equation E=mc², which seemingly explains a natural phenomenon with just three variables. Yet, diving deeper reveals far more complexity in the meanings of these variables. Scientific laws often have limitations in their explanatory power, leading us to discover more intricate laws over time. While we strive for simplicity at a local level, we simultaneously increase complexity on a global scale.
Could our notion of simplicity merely reflect an irrational human tendency? Or is there potential for an objective measure of simplicity in science?
Chapter 2: Navigating the Scientific Landscape
Imagine you are a scientist working on two distinct theories that explain the same phenomenon. If both theories hold equal validity but yield different predictions, which would you choose to test first? Most likely, you would opt for the simpler theory. But what does 'simplicity' truly entail? Like E=mc², 'simplicity' encompasses numerous factors.
You'd need to consider your available testing equipment, the funding required, and your own understanding of the topic. Suppose you could quantify these factors to define scientific 'simplicity' objectively. Such a definition could streamline future testing processes. However, several practical challenges arise. What is simple for you based on your background might be complex for someone else.
Before concluding our exploration of simplicity, let's take one last look.
Section 2.1: The Mathematical Quest for Simplicity
Now, let's step into the shoes of a mathematician. Suppose you need to determine which geometric shape is the simplest:
If you focus on the number of sides, the triangle is the simplest, as the circle can be viewed as a polygon with infinite sides. However, when calculating area, the triangle loses its title to the square, as its area is a function of a single variable (its side length). The area of a circle, however, involves π. While π is a beautiful symbol in mathematics, representing its value with integers requires an infinite series, thus complicating what appears straightforward.
In essence, even mathematics does not provide a clear path toward simplicity. So, what alternatives remain in our pursuit of understanding simplicity?
Section 2.2: The Future of Scientific Simplicity
From my observations, scientific discoveries seem to be growing in complexity over time. Mathematicians are increasingly challenged by the latest proofs, which are so intricate that few possess the expertise to verify them efficiently. This trend may be partially explained by entropy. Our human desire for simplicity aims to minimize local entropy in the present, yet over time, maximizing entropy appears inevitable.
For a non-technical introduction to entropy, feel free to check out my essay on its origins.
Returning to simplicity, although it holds a cherished place in the hearts of scientists and mathematicians, it seems to be more of a human construct than a scientific principle. Nevertheless, this pursuit serves a purpose: it simplifies our lives and enables us to employ the most efficient methods available.
Ultimately, it appears that no objective notion of simplicity truly exists. Yet, the subjective notion of simplicity may indeed be a valuable asset in our scientific endeavors!
The first video explores how Occam's Razor has influenced scientific thought, showcasing the importance of simplicity in understanding complex realities.
The second video features John Lennox discussing the reasons behind our existence and presenting scientific evidence for the divine, enriching the conversation around simplicity in science.