Chapter 1: Introduction to Missing Numbers

Can you uncover the elusive missing number? There exists a method to achieve this in mere seconds.

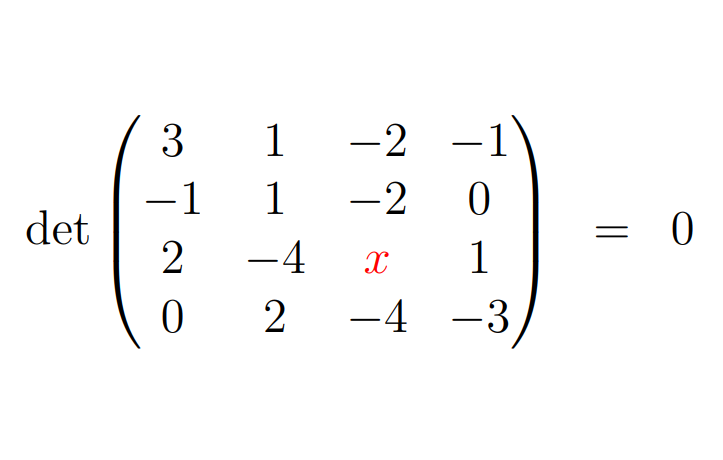
To find the value of x that results in a 4x4 matrix with a determinant of zero, one might typically perform a detailed determinant calculation. While this method is valid, it can be cumbersome, especially for larger matrices.

Fortunately, there's a more efficient approach borrowed from linear algebra principles:

If any linear dependencies exist among the columns (or rows) of the matrix, the determinant will be zero.

What does linear dependency imply?

It signifies that:

• One of the columns (or rows) consists entirely of zeros.
• One of the columns (or rows) can be expressed as a combination of the other columns (or rows).

A linear combination means that we can add and scale the columns to derive another column.

For instance:

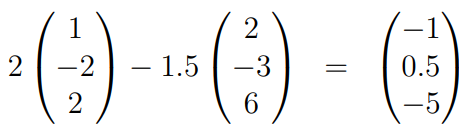
A matrix formed with these three vectors as its columns will yield a determinant of zero.

Key Insight: It's impossible to multiply all columns by zero.

I will clarify this method after we address the puzzle. Let’s revisit the 4x4 matrix:

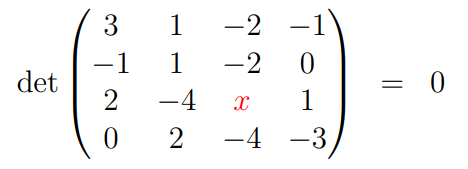
Pay attention to the 2nd and 3rd columns. Notably, aside from the variable x, the 3rd column is -2 times the 2nd column. This reflects a linear dependency, as we can scale the 2nd column to obtain the 3rd. Thus, we require x to equal -2 multiplied by -4:

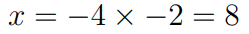
This resolves our problem.

Why does a linear dependency among the columns guarantee a zero determinant?

A matrix has a determinant of zero if it transforms a non-zero vector into the zero vector.

Here’s a brief notation to construct a matrix from its columns, using a 3x3 example:

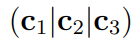
When a vector is multiplied by a matrix, the following occurs:

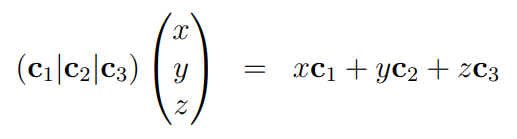
If a linear dependency exists among the columns, it indicates that one column can be expressed in terms of the others. We can rearrange the equation to place all terms on one side and the zero vector on the other:

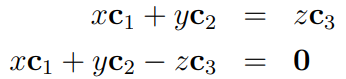
This can be represented as a matrix-vector multiplication:

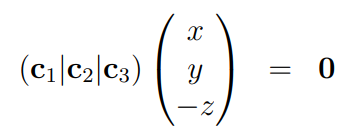
This results in a non-zero vector (x, y, -z) that the matrix maps to the zero vector, confirming that the determinant is zero. This principle extends to n x n matrices.

Challenge: I assumed another principle in my explanation: A matrix has a determinant of zero if and only if it maps a non-zero vector to the zero vector. Why is this assertion valid?

Hint: Consider attempting to invert it.

Chapter 2: Engaging with Puzzles

In this video, we explore a mathematical puzzle that challenges viewers to find the missing number in a square grid. It presents a fun and engaging way to apply the concepts discussed.

This video delves into finding the missing number in a series puzzle, providing viewers with a stimulating challenge that reinforces their understanding of mathematics.