Chapter 1: Introduction to Parabolas

Buckle up, we're diving into some algebra! In this guide, we will tackle problem #3 from page 142 of "Points, Lines, and Conic Sections" by Tony Berard, a book available on Amazon for just $15. You can find it [here](click here).

The problem presented is as follows:

3. Determine the equation of a downward-opening parabola with its focus located at (1, 1), intersected by a line with a slope of 2, and with a distance of three units between the intersection points.

How should we approach this problem? Our goal is to derive the equation of a parabola, which is generally expressed as y = ax² + bx + c. Consequently, we need to identify the values of three variables: a, b, and c.

We know the coordinates of the focus, which we can denote as F for focus: F(1, 1). This point is provided to us as a given—mathematicians do offer us something after all!

Next, we're informed that a line with a slope of 2 passes through this focus. This information allows us to formulate the equation of the line. Using the formula y - y₁ = m(x - x₁), we can derive:

y - 1 = 2(x - 1), which simplifies to y = 2x - 2 + 1 = 2x - 1. Thus, the line's equation is y = 2x - 1.

However, the standard parabolic equation doesn't seem to fit our needs well. There exists an alternative form: y = a(x - h)² + k, where h and k represent the x and y coordinates of the vertex. Unfortunately, we only have the focus coordinates.

If we label the intersection points between the line and the parabola as (x₂, y₂) and (x₃, y₃), we can create a system of equations utilizing the line's equation, either version of the parabola's equation, and a distance equation relating these two points. Setting up this system might look daunting, and solving it could be quite cumbersome.

At this point, we appear to have exhausted the traditional methods taught in schools. So, what now? Worry not! I will disclose an essential insight from the math book mentioned above. The chapter contains sufficient information for students to complete the exercises at the end.

There is a vital relationship among the slope, m, of the line through the parabola's focus, the constant, a, in either equation form of the parabola, and the distance, d, between the intersection points of the line and the parabola. This relationship can be expressed as follows:

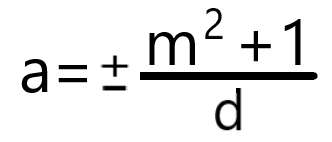
This original equation developed by the author helps simplify the problem. The equation is already solved for a, so we can simply substitute the right-hand side values. Since we need the equation for a downward-opening parabola, we select the negative sign in the equation. Therefore, we find a = -(2² + 1)/3 = -5/3.

Now that we have the value of a, and we already identified h and k, we can construct our final equation for the parabola as y = (-5/3)(x - 1)² + 1.

This effectively resolves the homework question derived from the book. Yet, we must verify our solution.

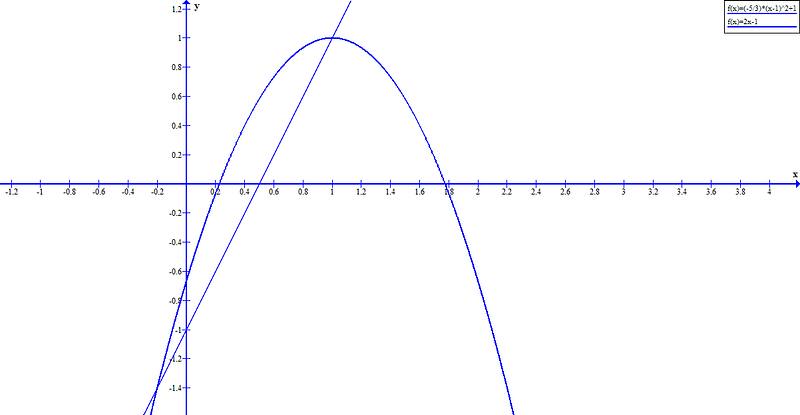
This image provides a graphical confirmation. It displays a zoomed-in view of the parabola and the line, showing that the distance between the intersection points is indeed three units. Should students wish to engage in more algebra, they can establish a system of equations involving the line and the parabola to identify the two ordered pairs. Plugging these into the distance formula will yield a distance of three units.

Thank you for joining me on this algebraic journey!

Chapter 2: Practical Applications in Algebra

In this video titled "100% Certainty you will see this in ALGEBRA," viewers will discover fundamental concepts and applications relevant to algebra.

The second video, "3. Algebra - BODMAS," provides an essential overview of order of operations, crucial for solving algebraic problems effectively.