Chapter 1: Understanding Trigonometric Sums

The roots of unity are incredibly helpful for determining specific values of trigonometric sums. In this section, we'll explore some examples to illustrate this concept.

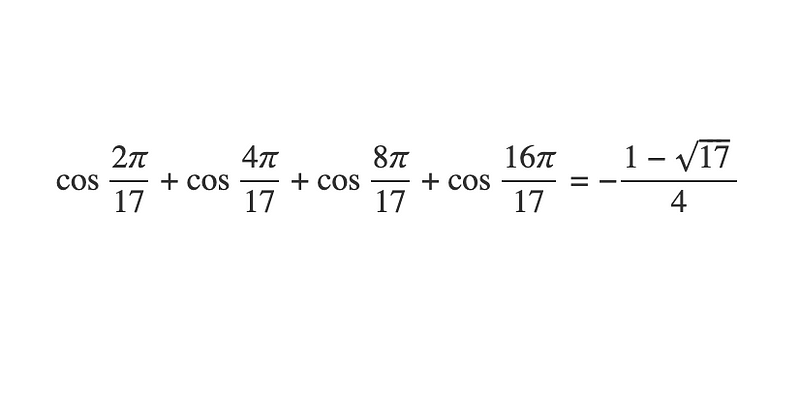
Later, I will demonstrate the validity of the aforementioned result. While it may initially seem random and complex, we can verify the accuracy through Python:

from math import cos, pi, sqrt

cos(2*pi/17) + cos(4*pi/17) + cos(8*pi/17) + cos(16*pi/17)

This yields:

> 0.780776406404415

And:

-(1-sqrt(17))/4

Also results in:

> 0.780776406404415

This confirms the correctness of our earlier calculation. Before delving into a mathematical proof, let's work through a simpler example.

Section 1.1: Evaluating a Basic Expression

To start, we will evaluate the following expression:

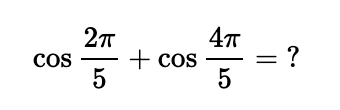
Let’s define ( theta = 2pi/5 ) and set ( y = cos theta + cos(2theta) ). Squaring ( y ) gives us:

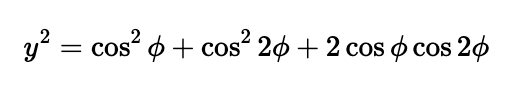
I will apply several trigonometric identities, specifically the following:

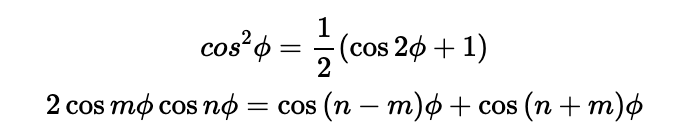
Substituting these into the equation for ( y^2 ) leads us to:

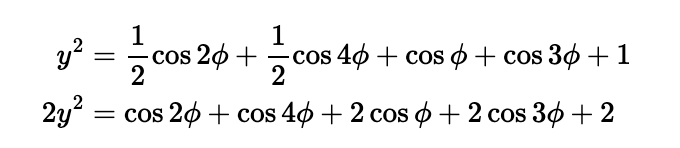
Returning to our value ( theta = 2pi/5 ), we note that ( cos(2pi/5) = cos(-2pi/5) = cos(8pi/5) ), thus ( cos theta = cos(4theta) ). Similarly, ( cos(2theta) = cos(3theta) ). Therefore, we can express:

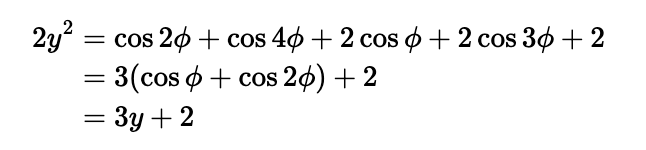
This simplifies to the quadratic equation ( 2y^2 - 3y - 2 = 0 ), which factors as ( (2y + 1)(y - 2) = 0 ). Thus, we find ( y = 2 ) or ( y = -frac{1}{2} ). Since ( cos theta ) and ( cos(2theta) ) must lie between -1 and 1, we conclude with:

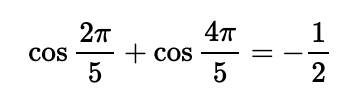
For those who favor computational verification, here's how it looks in Python (noting the floating-point approximation):

cos(2*pi/5) + cos(4*pi/5)

Results in:

> -0.4999999999999999

Section 1.2: Exploring Euler’s Theorem

You may have observed the symmetry in the trigonometric properties of the fifth roots of unity used in our solution. Recall Euler's theorem, which states:

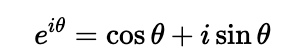
Using Euler's theorem, we can demonstrate that the sum of the real components of all n-th roots of unity equals zero:

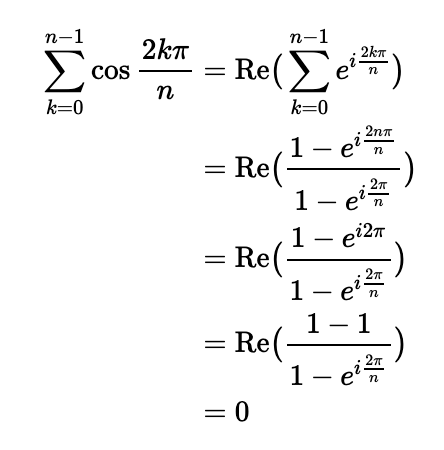
This insight will guide us into the next section, where we will specifically analyze the 17-th roots of unity to derive the result mentioned at the beginning.

Chapter 2: Proving the Initial Result

Let’s define ( theta = 2pi/17 ). To demonstrate our original result, we need to compute ( z = cos theta + cos(2theta) + cos(4theta) + cos(8theta) ). Squaring ( z ) leads us to:

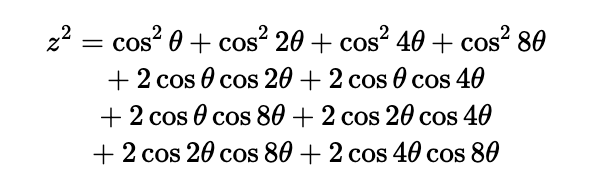
Don’t shy away from a little hard work. Utilizing earlier trigonometric identities, we can express:

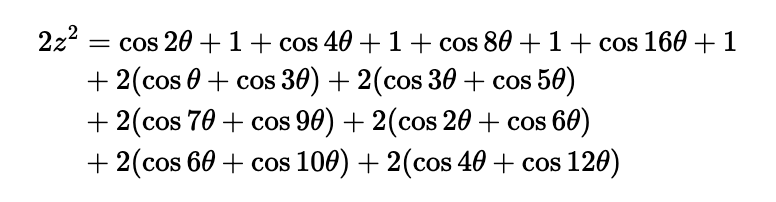
By grouping terms, we arrive at:

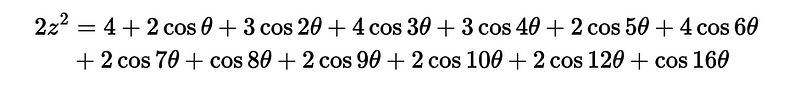
Adding ( z - 2 ) to both sides yields:

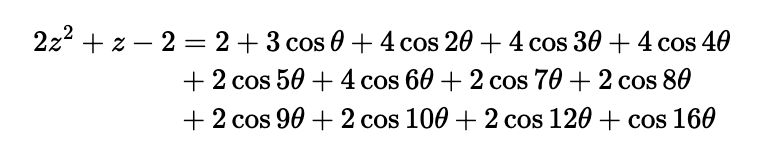
Recalling that ( theta = 2pi/17 ), we can simplify some terms using the symmetry of the 17th roots of unity. For instance, ( cos theta = cos(16theta) ), and so forth. This results in:

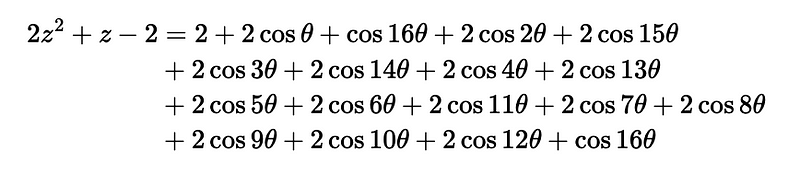
Grouping terms again shows that the right side is a multiple of the sums of the real parts of all the 17th roots of unity. Thus, we have:

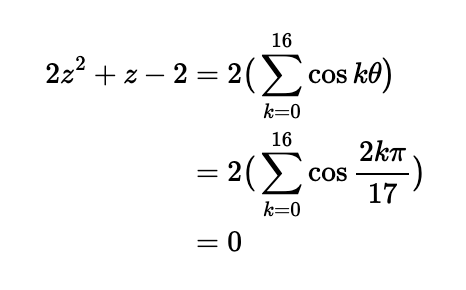
Finally, we solve ( 2z^2 + z - 2 = 0 ) using the quadratic formula, leading us to:

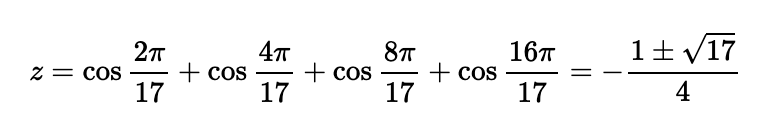
Among these roots, one is positive and the other negative. Considering that ( cos(2pi/17) ) and ( cos(16pi/17) ) have close magnitudes but opposite signs, and noting that ( cos(8pi/17) ) is near zero, we conclude that the dominant term is ( cos(4pi/17) ), which is positive. Therefore, our solution must be the positive root of the quadratic equation, leading us to our final conclusion.

What are your thoughts on this approach to calculating trigonometric sums? I invite you to share your insights!

Chapter 3: Video Resources for Further Learning

A tutorial on using sum and difference formulas to find exact cosine values.

An introduction to trigonometric identities for evaluating expressions, focusing on sum and difference identities.