Chapter 1: The Golden Integral Unveiled

In one of my earliest articles on Medium, I shared my admiration for what I thought was my favorite integral—the golden integral. However, it has since faced competition.

My preferred integral, often dismissed by traditional education, is surprisingly simple: π ≈ 22/7. By evaluating a straightforward integral, we can demonstrate that π ≈ 22/7, regardless of what we learned in school.

Let’s take a moment to refresh our memories. The golden ratio, φ, is the positive solution to the equation:

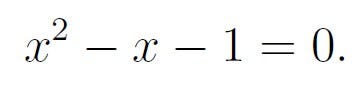
To elaborate:

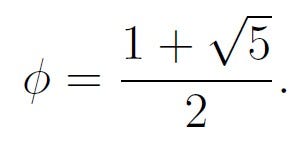
Many articles delve deeply into this topic, so I’ll keep it brief and shift my focus to the more intriguing golden integral.

At first glance, the golden integral may appear daunting, and its evaluation is not immediately clear. In this article, I’ll present one solution method. But before we dive in, we need to outline two key concepts that will be useful later.

1. The Golden Ratio Identity

As φ satisfies the equation x² - x - 1 = 0, we derive the following relationships:

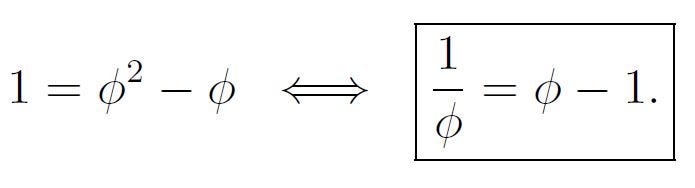
2. The Gamma and Beta Functions

For those unfamiliar with gamma and beta functions, they may seem complex and intimidating. No need to fret; I’ll only cover what’s essential for our discussion and highlight what you should remember for later use. These functions will play a minor role towards the end of our calculations.

In essence, the gamma function extends the factorial function to non-integer values. For any real number x > 0, it is defined by:

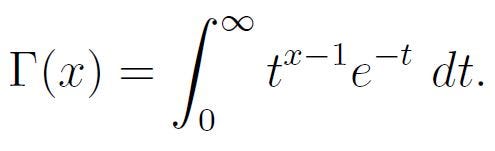
Key properties of the gamma function include:

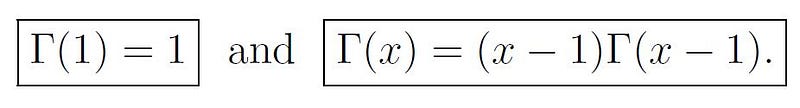
The beta function closely relates to the gamma function, as we will soon see. For any real numbers x, y > 0, it is defined by:

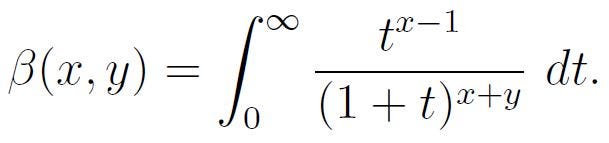
Remember the form of the beta function, as it will be relevant for our calculations, along with the following relationship between beta and gamma functions:

Now that we’ve established this foundation, let’s tackle our integral.

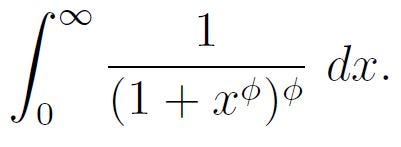
We will initiate our solution with a substitution. Let’s consider:

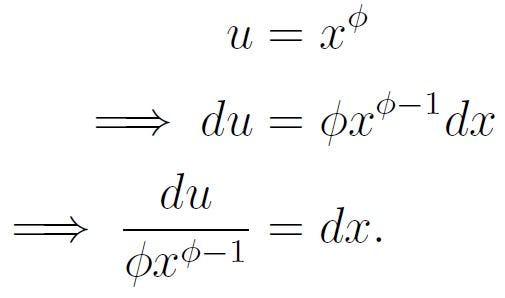
With this substitution, we can reformulate our original integral as follows:

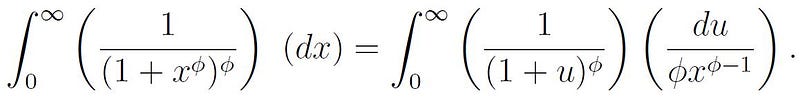
It's worth noting that we didn't need to alter the limits of integration, as:

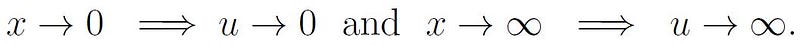
Next, we will replace the variable x in our new integral using the identity:

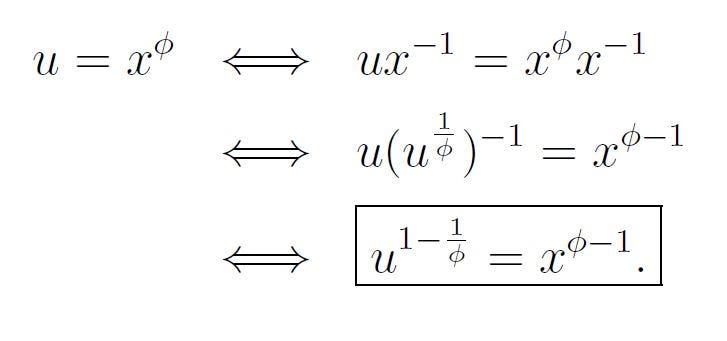
Thus, we arrive at:

In this expression, we utilized the golden ratio identity we discussed earlier. The next step requires recognizing that our function resembles the beta function mentioned above. Specifically, we can rewrite the integral as:

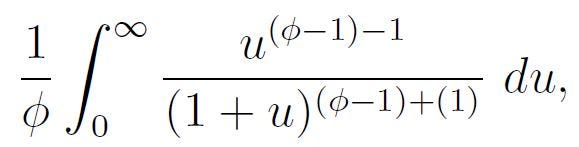
This clearly matches a beta function with x = φ - 1 and y = 1. In particular,

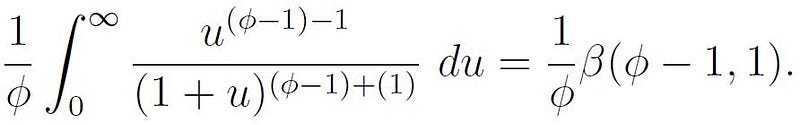
We can now leverage the relationship between the beta and gamma functions to evaluate this integral. Recall from earlier that:

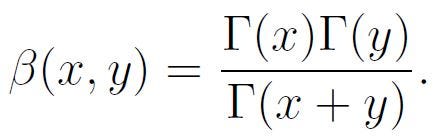
Consequently, we find:

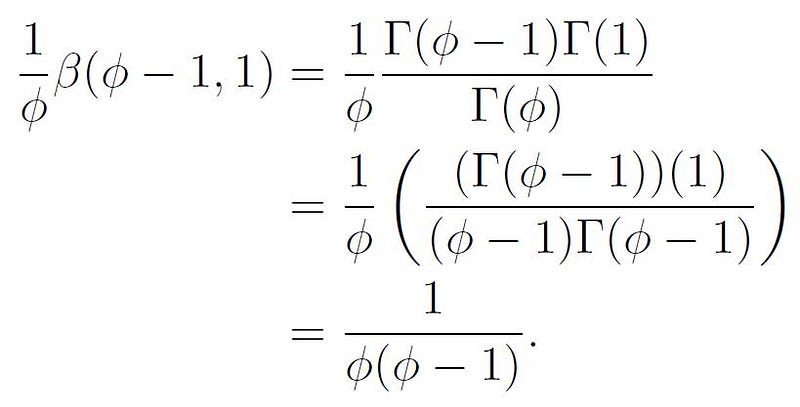
Note that we utilized the property Γ(x) = (x - 1)Γ(x - 1) mentioned previously.

As a final step, we should recall again that:

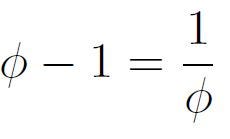
Thus, we conclude with:

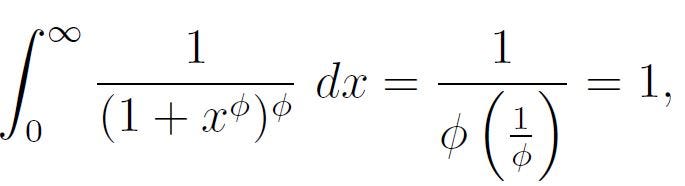
Isn’t that remarkable? I hope you found this exploration as captivating as I did. Students often ask me, “What kind of math brings joy to mathematicians?” For me, it’s uncovering unexpected results like this one.

An alternative approach to solving this integral involves the classic "tan substitution." Why not give it a shot?

Hint: Let

You can explore this solution in detail here:

An Alternative Solution to the Golden Integral.

Building on my previous article,

Thank you for reading. If you found this article valuable, I would greatly appreciate it if you would consider following me and my publication Y(Math) to help my work reach a broader audience.