Exploring the Intricacies of Star-Shaped Geometry Puzzles
Written on
Chapter 1: The Star-Pentagon Relationship
In the realm of geometry, consider the fascinating interplay of shapes: a star nestled within a pentagon, which in turn is encapsulated by another star, and so forth. Imagine this sequence extending infinitely, both outward and inward. What intriguing patterns might emerge?
This presents an engaging and stimulating geometry challenge for you. Here’s a hint: the stars are constructed from triangles. Take a moment to pause, grab your pen and paper, and tackle this puzzle before you continue for the solution!
Solution
The essence of this puzzle lies in the properties of the triangles involved. Notably, triangles AGB and CHJ are both isosceles and congruent.
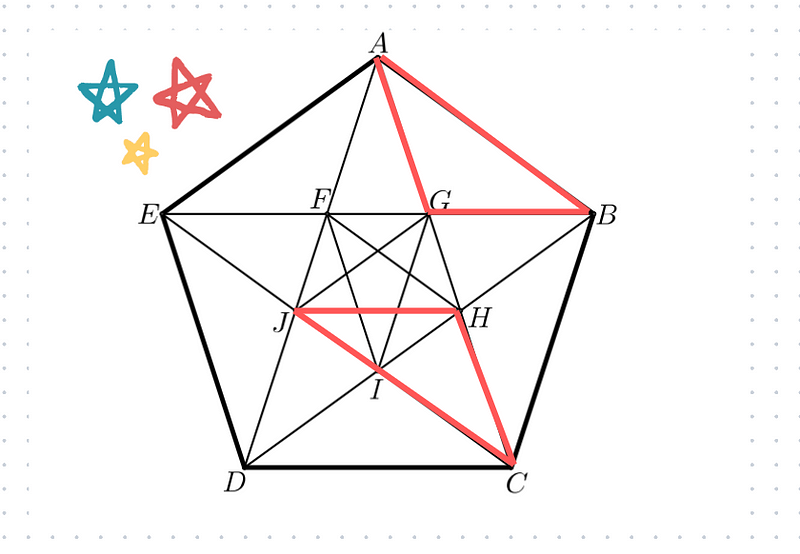
This congruence implies that AG = GB = HC = HJ = 1, as stated in the problem. Furthermore, triangles AFG and BGH also share congruence.
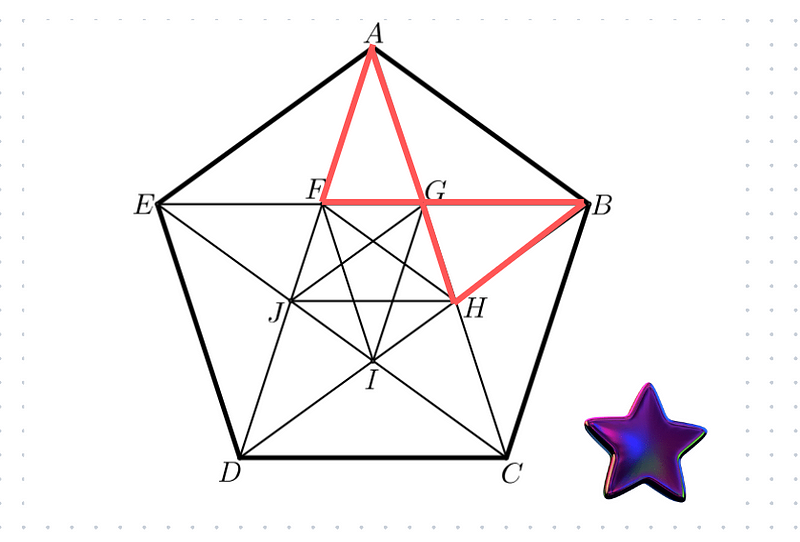
Thus, we can conclude that FG = GH as well. Finally, triangles AGDF, AHJ, and ACD are similar, with each triangle fitting within the larger one, resembling a cascading effect.

To illustrate, we have labeled the triangle lengths as a, b, c, and d. Our aim is to find the sum of b, c, and d. By leveraging the similarity of these triangles, we derive the equation:
a/b = (a + b)/c = (a + b + a)/d
This equation serves as a foundation for the algebraic manipulations that follow.
Continuing the Math
Given AG = 1 and recognizing that a = c, we find that:
a = c = 1
Substituting these values into our earlier equation, we simplify to obtain:
1/b = (1 + b)/1
This leads us to the quadratic equation:
b² + b - 1 = 0
Excluding the negative solution, we find:
b = (√5 - 1)/2
Having established the values of a, b, and c, we can substitute them back into our equation:
1/((√5 - 1)/2) = (2 + (√5 - 1)/2)/d
Refer back to the previous equation if needed. Ultimately, we deduce that:
d = (1 + √5)/2
Thus, we arrive at our final answer:

And that concludes our solution.

Isn't it fascinating? What were your thoughts during this puzzle? I would love to hear your insights in the comments below!
Math Puzzles
Discover a collection of intriguing math puzzles on Medium, covering various topics such as Algebra, Geometry, Calculus, and Number Theory. Share this with your friends to challenge them too!
The first video, "How to Sum a Column or Cells in Apple Numbers," provides valuable insights into using Apple Numbers for your calculations.
The second video, "Excel: Sum Across Multiple Columns With One or More Criteria - 3 Methods," discusses various methods for summing data in Excel, enhancing your spreadsheet skills.
Thank you for reading! If you found this article insightful, please consider showing your appreciation by clapping.

If you’d like to support my writing, consider buying me a coffee! Your generosity helps sustain my work and academic pursuits.
Happy Solving, Bella