Exploring a Japanese Math Challenge from the Isaniwa Shrine
Written on
Chapter 1: Introduction to Sangaku
This intriguing mathematical puzzle originates from the Isaniwa Shrine in Matsuyama, the largest city in Shikoku, and is dated back to 1937. The challenge involves a configuration of circles, where the smallest circle has a radius of 1. Your task is to determine the radius of the largest outer circle in terms of the radius of the central red circle.
Before you proceed, I encourage you to pause and attempt the problem with pen and paper. Once you're ready, continue for the solution!
This video provides an engaging explanation of the famous math problems related to Japanese temple geometry.
Section 1.1: Hint and Initial Thoughts
To start, imagine the small circle has a unit radius (1), while the four adjacent circles share a radius denoted as r. The relationship between the outer circle's radius (R) and the radius of the smaller circles can be expressed as R = 2r + 1.

Section 1.2: Applying Pythagorean Theorem
Next, we can utilize Pythagoras’ Theorem to derive further insights into the relationships between the circles.
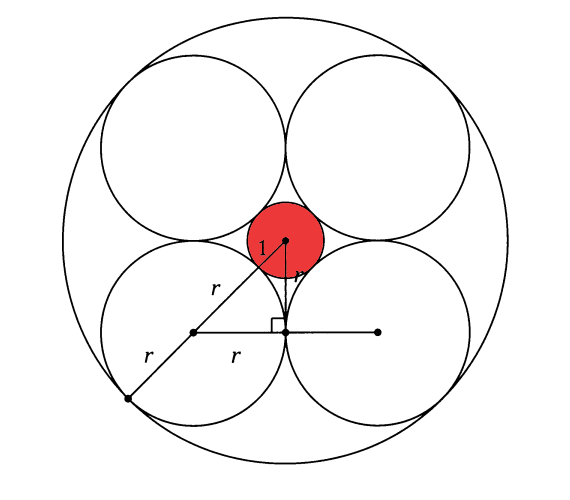
Subsection 1.2.1: Solving the Equation
By employing the quadratic formula, we can find the value of r.
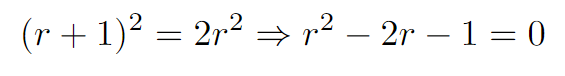
As we simplify, we observe that we discard r = 1 - √2. With the radius of the surrounding circles established, we can rearrange the quadratic equation for further insights.
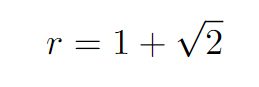
From our earlier equation, we know that R = 2r + 1, leading us to our final answer.

And that concludes our solution!
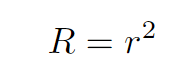
Isn't it fascinating?
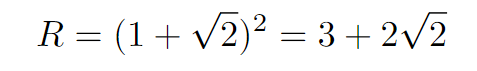
I'd love to hear your thoughts on this challenge! How did you approach the problem? Please share your insights in the comments below.
This video presents a tricky math question from Japan, further enhancing your understanding of these complex problems.
Math Puzzles
Explore a collection of intriguing puzzles, including topics like Algebra, Geometry, and Calculus. Share these challenges with friends and family to spark engaging discussions!
Thank you for reading! If you found this article helpful, please consider showing your appreciation.

If you're interested in personalized math puzzles, feel free to reach out!
Love, Bella