Zeroes of Homogeneous Polynomials

To begin, let’s consider homogeneous polynomials involving three variables with rational coefficients. A homogeneous polynomial is defined as one in which all terms share the same degree. For instance, (x^2 + frac{1}{2}y^2 - z^2) is a polynomial of degree 2, while (x^3 + xyz + yz^2) is of degree 3.

On the other hand, polynomials like (x^2 + y + xz^3 + 1) do not qualify as homogeneous due to differing degrees among terms. We will focus on rational solutions when these polynomials are set to zero.

If (p(x,y,z)) is a polynomial, a rational solution refers to a triplet ((a,b,c)) of rational numbers satisfying (p(a,b,c) = 0). For example, the polynomial (x^2 - z^2) admits the rational solutions ((1,0,1)) and ((1,1,1)), among others.

Here are two key properties of homogeneous polynomials:

1. Property 1: If the degree is at least 1, the solution ((0,0,0)) is always valid. You can verify this by examining the polynomial's structure.
2. Property 2: If ((a,b,c)) is a rational solution, multiplying this solution by any rational number yields another rational solution. Essentially, this implies that finding rational solutions is equivalent to identifying integer solutions, as we can scale by the denominators of (a), (b), and (c).

This second property motivates our exploration in projective space, where we disregard ((0,0,0)) and treat multiples of ((a,b,c)) as equivalent.

Low Degree Examples

Let’s explore distinct rational solutions in some low-degree scenarios.

Degree 1 is straightforward and has infinitely many distinct rational solutions. For instance, if (p(x,y,z) = x - y - z), setting (z = 1) leads to (x = y + 1), enabling us to generate an infinite set of solutions like ((a+1, a, 1)) for any rational (a).

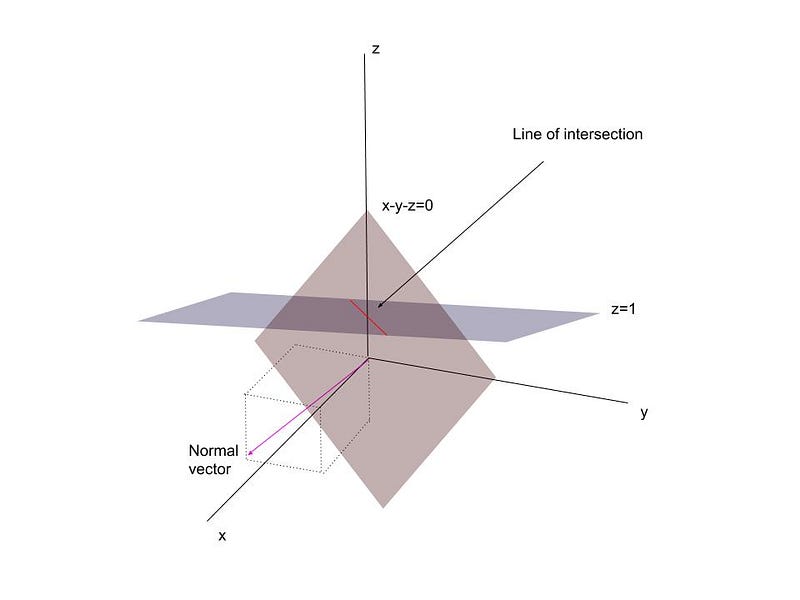
Geometrically, the equation (x - y - z = 0) describes a plane, and by setting (z = 1), we are essentially intersecting this plane with another, which leads to a line of solutions.

When examining degree two, we encounter the polynomial (x^2 + y^2 - z^2 = 0), which is known to have infinitely many rational solutions, related to the existence of Pythagorean triples.

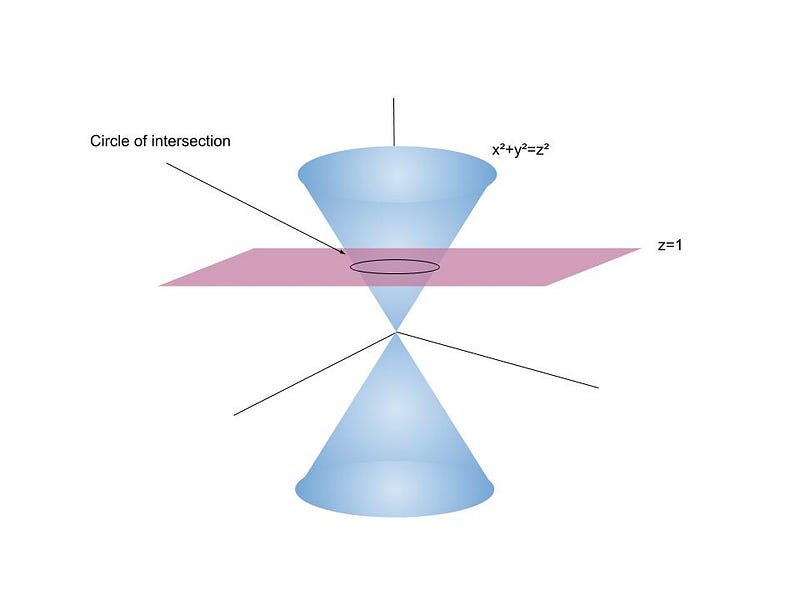
As we set (z = 1), we transform our problem to finding rational points on the unit circle defined by (x^2 + y^2 = 1), which is well-documented to have infinitely many rational solutions.

However, some degree 2 polynomials, such as (x^2 + y^2 + z^2), do not yield rational solutions without introducing complex numbers. Adjoining a single root (like (i) from (x^2 + 1)) allows us to find infinitely many solutions.

Faltings’s Theorem and Fermat’s Last Theorem

Now, we can present a modified version of the Mordell conjecture established by Faltings. Consider a homogeneous polynomial (p(x,y,z)) in (mathbb{Q}[x,y,z]) that is "smooth." While this condition might seem intricate, it relates to the geometric nature of the theorem and is easily verified through standard calculus techniques.

Theorem: If the degree of (p(x,y,z)) exceeds 3, there exist only finitely many distinct rational solutions. Additionally, infinitely many solutions cannot be obtained by adjoining a finite number of polynomial roots to (mathbb{Q}).

This theorem offers a weak version of Fermat’s Last Theorem, as the equation (x^n + y^n = z^n) for (n geq 4) only admits finitely many integer solutions.

In this context, we will consider the implications of this theorem on non-homogeneous polynomials by substituting (z = 1) as demonstrated in earlier examples.

The first video, "The Mordell Conjecture 100 years later," explores the historical significance and implications of this conjecture.

Topology and Geometric Insights

We've been addressing the task of finding integer solutions to polynomials, but this approach leads us to a more geometric perspective. Transitioning to geometric analysis over (mathbb{R}) allows us to utilize familiar tools from calculus and linear algebra.

This method is foundational in a field known as "arithmetic geometry," where we connect rational solutions of polynomials with the geometry of curves in projective spaces.

As we delve deeper, we note that the topology of these curves can be characterized by their genus. For example, a degree 2 polynomial will yield a sphere (genus 0), while a degree 3 polynomial corresponds to a torus (genus 1).

The relationship between the degree of a polynomial and its genus is encapsulated in the Genus-Degree Formula, revealing the fascinating interplay between algebra and topology.

De Franchis Theorem

The comprehensive proof of Faltings's Theorem is intricate and involves numerous insightful concepts, but I will summarize why the genus is a crucial factor.

In the context of complex analysis, compact Riemann surfaces are classified into three types based on their genus:

• Genus 0 corresponds to elliptic curves (spheres).
• Genus 1 pertains to parabolic curves (donuts).
• Genus greater than 1 is designated as hyperbolic.

The geometric distinction between these cases is essential for understanding why there are only finitely many rational points on curves of genus greater than 1.

The main result relevant to this discussion is:

Theorem: For curves (X) and (Y) with genus greater than 1, the set of non-constant functions (f: Y to X) is finite, as articulated in the de Franchis Theorem.

This classification underscores the complexity of curves and their associated properties.

Changing the Problem: A New Perspective

Let’s now shift our focus. Given a polynomial (q(x,y,z)), its zero set forms a curve (C). By considering this curve within complex projective space, we can derive a new perspective on rational solutions.

Each rational point on the curve (C) can be associated with a unique geometric object. The essence of this approach lies in demonstrating that only finitely many distinct rational points correspond to the same geometric object, effectively transforming the problem.

Every curve (C) has an associated (g)-dimensional space known as the Jacobian variety, (Jac(C)). This space possesses an additive structure, enabling us to explore the relationships between rational points on the curve.

The application of the de Franchis Theorem helps establish that only finitely many distinct rational points on (C) can yield the same Jacobian variety, thus leading to the conclusion that there are only finitely many curves of a specific genus.

Faltings's comprehensive proof involved several iterations of this reduction process, ultimately demonstrating the validity of the Mordell Conjecture.

In recognition of this monumental achievement, Faltings received the Fields Medal in 1986, solidifying his legacy in the mathematical community.

The second video, "Faltings's theorem," delves into the details of Faltings's proof and its implications for modern mathematics.