# The Economic Impact of Foreseeing the Future: A Game Theory Perspective
Written on
Understanding Game Theory and Its Applications
Game theory, a mathematical framework with numerous applications, significantly influences economics. This is why many mathematicians receive the Nobel Prize in Economics. A prominent figure in this field is John Forbes Nash, whose life was depicted in the film "A Beautiful Mind."
Let's illustrate game theory with a straightforward example.
Simple Game Dynamics
Imagine two players, Alice and Bob, along with a game master. The rules are simple: each player can choose to either contribute €8 to the game master or opt out entirely. Their choices are made without knowledge of the other's decision. The game master collects the contributions, which can total either €0 (if both abstain), €8 (if one contributes), or €16 (if both contribute). This amount is then increased by 50% and shared equally between Alice and Bob.
For instance, if both Alice and Bob decide to contribute €8, the total becomes €16, which, after a 50% increase, totals €24. They then split this equally, resulting in each earning €4. However, this scenario is just one possibility. Let's analyze all potential outcomes.
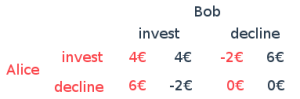
Evaluating Strategies: A Closer Look
Upon examining the game's structure, a pattern emerges. If Bob decides to invest, Alice's optimal choice is to abstain, and vice versa. Thus, in this perfectly rational scenario, both players would ultimately choose not to invest, missing out on potential rewards.
This situation mirrors real-life scenarios, such as group projects in school, where individuals hesitate to contribute due to fear of unequal workload distribution. If everyone were to pitch in, they would achieve a better outcome together.
Exploring the Possibilities
Why is this game important? Is there a way for Alice and Bob to collaborate and profit? Yes! The dynamics change significantly when the game is played over multiple rounds. The variety of strategies increases exponentially, allowing for more complex decision-making. For instance, Bob might choose to decline every other round while investing in the others. The lack of knowledge about the final round is crucial; if players knew when the last round would be, they would default to avoiding investment in anticipation of the end.
This principle applies to real-world economic interactions, such as the job market within a social economy where unemployed individuals receive benefits. Each month, individuals must decide whether to invest their time, and knowing the endpoint would undermine the system's functionality.
Determining Optimal Strategies
Returning to our game, what constitutes the best strategy? A multitude of strategies exists, varying in complexity. One might even invest based on mathematical patterns, but the optimal approach is surprisingly simple:
- Invest in the first round.
- For subsequent rounds, mimic the previous action of the other player.
Why does this work? If Bob adopts this strategy and Alice consistently declines, Bob only incurs a loss in the initial round but secures himself thereafter. If Alice opts to invest, Bob follows suit, ultimately resulting in mutual gains. This adaptability ensures that Bob’s losses remain minimal while maximizing potential earnings if Alice participates.
If you found this exploration intriguing, feel free to follow me (Marcel) on Medium for more insights!
The Bottom Line: The Risks of Predicting the Future
Understanding the implications of foreseeing future events can shed light on why our economic systems thrive on uncertainty. Without that element of unpredictability, the delicate balance could easily tip into chaos.