Chapter 1: Introduction to Proportional Control

Proportional control is a fundamental concept in control systems, crucial for maintaining desired outputs in various applications. This method traces its origins back to the 1920s, thanks to the pioneering work of Nicholas Minorsky, a Russian engineer. He first articulated the notion of proportional control in his studies on automatic ship steering, highlighting the importance of stabilizing feedback.

Minorsky's seminal paper, published in 1922, proposed that a feedback controller could effectively stabilize a system by ensuring that the system's response correlates directly with the error signal. The recognition of proportional control expanded significantly in the 1930s and 1940s, primarily due to Harold S. Black's contributions. His development of negative feedback amplifiers laid the groundwork for the widely adopted proportional-integral-derivative (PID) controllers used in industrial settings today.

For additional insights, refer to:

• Minorsky, N. (1922). Directional Stability of Automatically Steered Bodies. Journal of the American Society of Naval Engineers, 34(2), 280–309.
• Black, H. S. (1934). Stabilized Feedback Amplifiers. Bell System Technical Journal, 13(1), 1–18.

Section 1.1: Mathematical Foundation of Proportional Control

The proportional controller, commonly referred to as the P-controller, utilizes a proportional gain constant, denoted as k?, to generate the output signal based on the error between the desired setpoint and the actual process variable. In essence, a larger error results in a greater output signal.

The mathematical representation of the output signal (u) is given by:

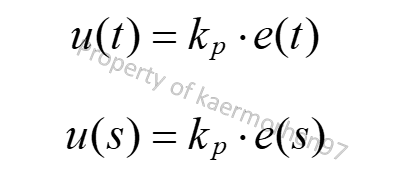
Where:

• u signifies the controller output.
• k? represents the proportional gain constant.
• e indicates the error, the difference between the setpoint and the process variable.
• t denotes time.
• s represents the Laplace transform.

Advantages of Proportional Control

1. Simplicity: The proportional controller is straightforward, featuring a single tuning parameter, making it easy to implement without requiring complex algorithms.
2. Rapid Response: This control method reacts quickly to changes in the process variable, making it ideal for applications like temperature and motor speed control.
3. Stability: It maintains stability across a broad spectrum of system parameters, provided the gain is appropriately set.
4. Robustness: Proportional control effectively handles variations in system parameters, responding promptly to changes in system conditions.

For further exploration, consider:

• 7. 6. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems. Prentice Hall, 2002.
• 14. 19. Nise, Control Systems Engineering. Wiley, 2011.
• 13. King and R. Katebi, Process Control: A Practical Approach. Springer, 2014.

Disadvantages of Proportional Control

1. Steady-State Error: This type of controller may exhibit a steady-state error, which is the persistent difference between the desired setpoint and the actual process variable.
2. Sensitivity to Parameter Variations: Changes in system parameters can lead to oscillations or instability if the gain is not optimally set.
3. Limited Control Authority: The controller cannot adequately compensate for significant disturbances, as its output is directly tied to the error.
4. Challenges with Non-Linear Systems: Proportional control may not be suitable for non-linear systems due to the lack of a direct proportional relationship between input and output.

For comprehensive insights, check:

• 7. 6. Franklin et al., Feedback Control of Dynamic Systems. Prentice Hall, 2002.
• 14. 19. Nise, Control Systems Engineering. Wiley, 2011.
• 13. King and R. Katebi, Process Control: A Practical Approach. Springer, 2014.

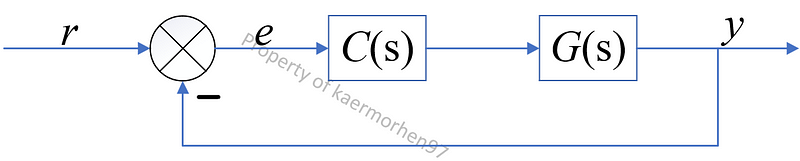
Understanding Steady-State Error in Proportional Control

The persistent steady-state error associated with proportional controllers can be illustrated through system diagrams and methodologies.

Practical Advice for Implementing Proportional Controllers

1. Balance Gain Carefully: The gain parameter critically affects the controller’s response. Excessively high gain can lead to instability, while low gain may result in sluggish performance.
2. Consider Adding a Dead-Band: To mitigate overreactions to minor disturbances, implementing a dead-band can help manage noise in the process variable.
3. Account for Saturation: When dealing with significant errors, it’s crucial to set saturation limits to prevent the controller from becoming inactive.
4. Manage Time Delays: Recognizing potential time delays between the controller's output and the process variable's response is essential for maintaining stability.
5. Acknowledge Non-Linearity: Non-linearities in the system may hamper performance, suggesting the use of more advanced control strategies, such as PID controllers.

Chapter 2: Practical Applications and Additional Learning

Explore the concepts of PID theory in practice with this video: PID Theory and Practice Part 3: P, I, PI Control of Speed. This resource provides a detailed overview of how proportional control integrates with other control methods.

Delve into the real-world applications of proportional control in this video: Desktop Process PLC Control (Part 3) – Proportional. It illustrates the practical implementation of these control principles.

Support my work:

Implementing Proportional Controllers in C++