Understanding Length Contraction in Einstein's Relativity Theory
Written on
Chapter 1: The Concept of Length Contraction
Length contraction refers to the relativistic effect where an object's length appears diminished from an observer's perspective when it is in motion. This phenomenon is only noticeable in the direction of the object's movement and becomes significant when its speed approaches that of light.

In 1905, while serving as an assistant examiner at the Swiss Federal Office for Intellectual Property, Albert Einstein released four groundbreaking papers in the journal Annals of Physics. One of these papers, titled "On the Electrodynamics of Moving Bodies," laid the foundation for his special theory of relativity. To reconcile the equations of electromagnetism with the mechanics of his time, Einstein made revolutionary modifications to Newton's notions of space and time.

Chapter 2: The Core Principles of Special Relativity
In a previous article discussing time dilation, I outlined the two main postulates of special relativity, which I will restate for clarity:
- Principle of Relativity: No experiment can determine an observer's absolute velocity; thus, the outcomes of experiments are not influenced by the observer's speed relative to others.
- Universality of Light Speed: The speed of light (denoted as c) remains constant for all observers, regardless of the relative motion between the observer and the light source.
To illustrate measurements in spacetime, Einstein envisioned a grid comprising clocks and rods, as depicted below:

Chapter 3: Analyzing Length Contraction
Imagine a train moving at velocity v, equipped with a lamp and a mirror. For someone inside the train, the signal from the lamp takes a specific time to bounce back to the mirror.

An external observer, however, will calculate the time taken for the light signal to reach the mirror and come back, as shown below:
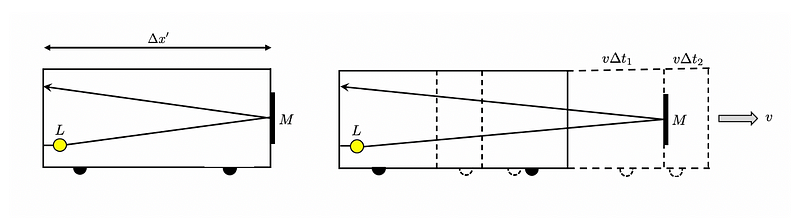
This observer must consider the train's motion, which affects the distance traveled by the light during its return trip.
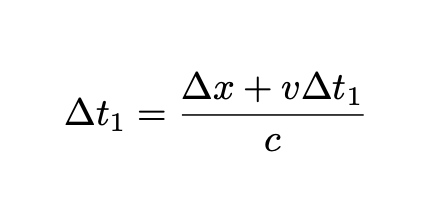
The total time for the light's reflection, as perceived by the external observer, can be summarized as follows:
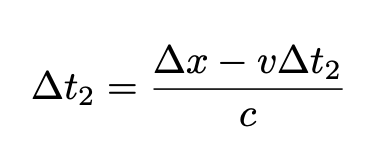
Using the time dilation equation from my earlier article, we arrive at:
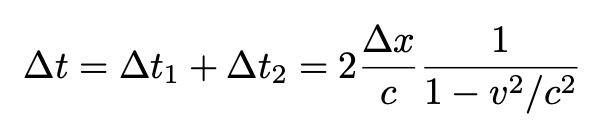
The resulting equation illustrates Lorentz contraction, showing how the lengths observed differ for moving objects.

For instance, consider a rotating wheel where the contact point with the ground has a velocity of zero. The length contraction occurs at the upper part of the wheel, where velocity is greater than zero. This behavior is effectively illustrated in the animation below.

Ultimately, we find that the observed distances are shorter for an external observer than for one at rest.

The equation for Lorentz contraction can also be derived through Lorentz transformations, similar to the method discussed in earlier articles.
Thank you for reading! Your feedback and thoughts are always appreciated. For more insights on physics and other topics like mathematics, machine learning, and finance, feel free to visit my LinkedIn, personal website at www.marcotavora.me, or my GitHub profile.
The first video titled "Length contraction: the real explanation" provides an in-depth analysis of this phenomenon, expanding on the concepts discussed in this article.
The second video, "Length Contraction and Time Dilation | Special Relativity Ch. 5," further explores the relationship between these two critical aspects of Einstein's theory.