The Foundation of Force and Motion

We begin with Newton's Second Law, often referred to as the Momentum Principle. This principle states that the total force acting on an object alters its motion. In equation form, it can be represented as follows.

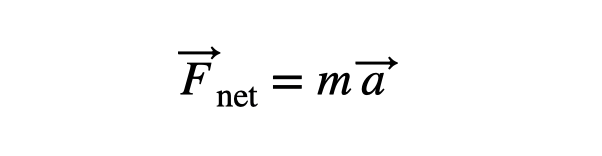
When a constant force is applied to an object, it experiences a consistent acceleration. This implies that the object's speed can increase, decrease, or change direction. Take a look at this example with a cart experiencing a constant force.

Now that we have covered the basics, let's delve into centripetal force.

Centripetal Force Explained

To understand centripetal force, we should first dissect the term itself. "Centripetal" means "center-seeking." Thus, this force directs an object toward the center of its circular path. Revisiting Newton’s Second Law, you may notice that the symbols for force (F) and acceleration (a) are represented as vectors, indicating they have multiple dimensions. This leads us to the vector definition of acceleration.

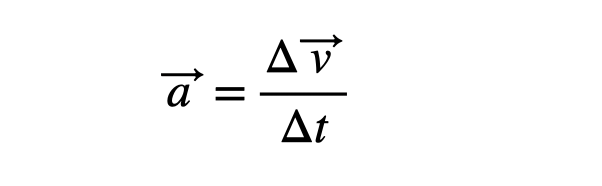
In physics and mathematics, the symbol ? (Delta) signifies "change in." Therefore, acceleration can also be expressed as:

As long as the velocity vector changes, acceleration is present. For instance, observe this animation of a ball being swung in a horizontal circle.

Here’s a diagram showing the ball at two different positions.

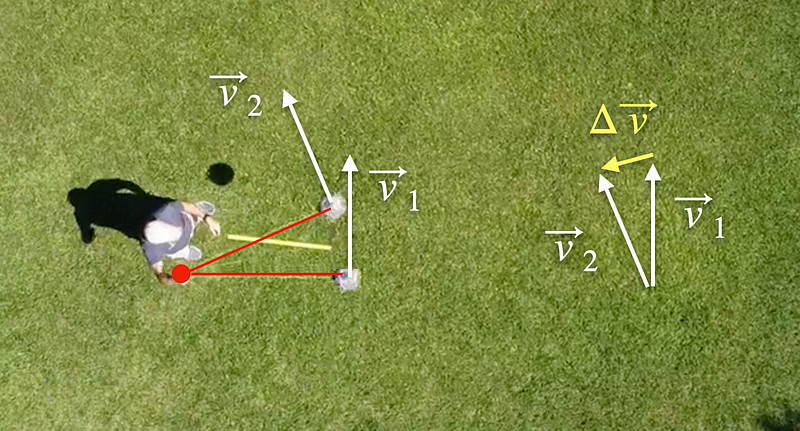
While the speed remains consistent at these two points, the direction alters, resulting in a change in velocity. The difference between the two velocity vectors points toward the center of the circle, which reinforces the concept of centripetal force (derived from centripetal acceleration).

To quantify this centripetal acceleration, while I won't delve into the derivation here, you can derive the following formula.

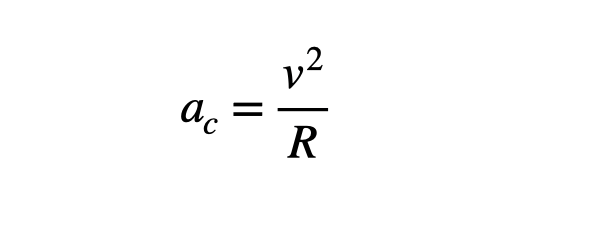
In this equation, R represents the radius of the circular path. If you multiply this centripetal acceleration by the object's mass, you obtain the centripetal force.

It's essential to clarify that centripetal force is not a distinct force; rather, it represents any force that causes an object to accelerate toward the circle's center. For the swinging ball, the centripetal force is provided by the tension in the string, while for a car navigating a curve, it results from the friction between the tires and the road.

Understanding Fake Forces

Before diving into centrifugal force, we must first address the concept of fake forces. Returning to the relationship between total force and acceleration, it's crucial to note that this principle only holds true in an inertial reference frame—essentially a non-accelerating viewpoint.

Consider the following example: a cart is being pulled by a spring that’s stretched by another cart with a fan.

In this scenario, the second cart accelerates to the right under the influence of a net force. A force diagram for this cart would look like this.

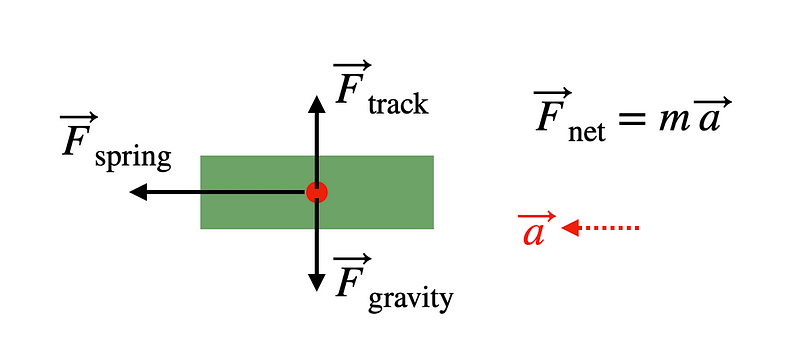
Here, the vertical forces cancel out, leaving only the force from the spring that causes the acceleration.

Now, imagine you are moving alongside the cart (or perhaps even riding on it). In this case, your perspective is that of the cart itself, which is not accelerating. If you were to analyze the forces without considering acceleration, you would need to introduce a fake force to maintain equilibrium.

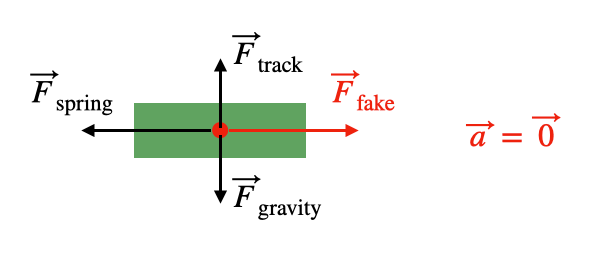
The magnitude of this fake force is contingent upon the object's mass and the acceleration of the reference frame, and it acts in the opposite direction of the frame’s acceleration.

People often mistake fake forces for real ones. They can feel quite genuine. For example, when a car accelerates forward, you might feel pushed back into your seat. However, no actual force is causing this sensation; it merely mimics the effects of a sideways gravitational force.

According to Einstein's equivalence principle, distinguishing between gravitational force and the effects of an accelerating reference frame is impossible.

Centrifugal Force Clarified

Now, let's explore centrifugal force. The term "centrifugal" translates to "center-fleeing," indicating a force that directs away from the circle's center.

Here’s another video illustrating this concept. It features a truck navigating a circular path.

If you were inside the truck while it turned left, you would observe the following scenario.

You might wonder why the string appears to hang to the right. What force is causing this? In reality, there is no force acting upon it. However, from the viewpoint of an accelerating reference frame, a centrifugal force appears to push outward from the center. This concept can be better understood through the following force diagrams.

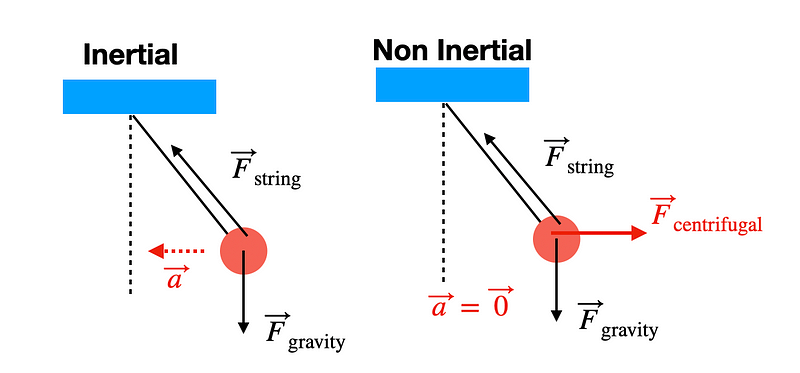
From an inertial reference frame (such as standing outside the vehicle), you would see the mass at the end of the string accelerating in a circular path, with the horizontal component of the tension in the string acting as the centripetal force.

Conversely, from inside the vehicle, the hanging mass appears stationary, necessitating the introduction of a centrifugal force to keep the forces balanced.

In conclusion, this clarifies the distinction between centripetal and centrifugal forces.

The Perception of Centrifugal Forces

It's important to note that forces themselves are neither good nor bad—they simply exist. However, many students have been cautioned against using the term "centrifugal."

The reason for this caution is that students often find the concept of centrifugal forces appealing. Yet, many struggle to identify real forces in physics. For instance, if you throw a ball into the air, a common misconception is that a "throw force" or "velocity force" propels it forward. In reality, no force pushes it forward; it continues moving due to inertia.

Introducing the idea of fake forces can complicate matters, especially since students often have difficulty grasping the nature of real forces.

Nonetheless, fake forces, like centrifugal force, can be beneficial in specific contexts—they just require careful handling, much like scissors are useful yet potentially hazardous. Always remember to proceed with caution when dealing with these concepts.