The Intriguing Journey to the Calculation of Pi: A Mathematical Saga
Written on
Chapter 1: The Enigma of Pi
The captivating narrative surrounding the value of pi (π) is omnipresent, yet many remain unaware of the complex journey leading to its accurate determination.

Photo by Max van den Oetelaar on Unsplash
A significant question in mathematics persists: Is π a normal number? This inquiry involves demonstrating that its decimal representation is statistically random. If proven, π would encapsulate every conceivable digit sequence, including the entire text of the Bible encoded within its decimals. But what exactly is this enigmatic number, and how did we learn to quantify it?
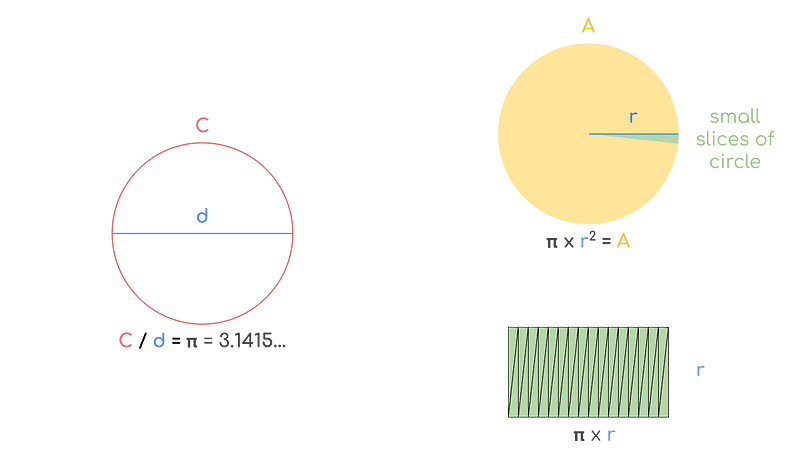
Defining π and the area of a circle — Image from Alessandro Visintin
Understanding π (pi)
Most individuals have encountered the term π at least once, whether during geometry lessons or through iconic quotes in influential films. π represents a mathematical constant that signifies the ratio between a circle's circumference (C) and its diameter (d). Thus, the Greek symbol stands for a value that is approximately 3.1415. It also appears in the formula for the area of a circle (πr²). To visualize this concept, think of dividing a circle into small segments and rearranging them into a rectangular shape. The rectangle's length would be πr and its height r. But why has this specific value garnered such fame? As an irrational number, π cannot be expressed as a fraction of two integers, prompting mathematicians over the centuries to seek increasingly accurate approximations.
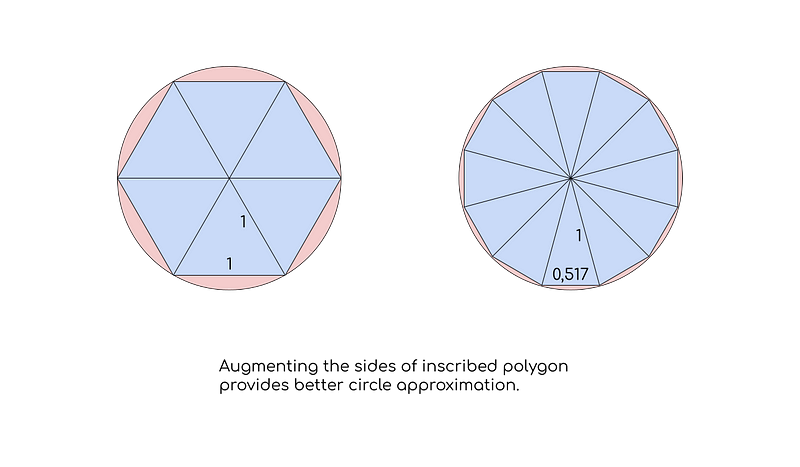
Approximating a Circle with Polygons
Let's consider a circle with a radius of 1. As previously established, its circumference is 2π. How do we estimate π's value? One method involves inscribing a hexagon within the circle and calculating its perimeter. With each side measuring 1, the total perimeter equals 6. Thus, our initial approximation gives 2π = 6, or π = 3. While this is a rudimentary calculation, it's a solid starting point. To enhance our estimate, we can divide the hexagon into a dodecagon and repeat the process. The dodecagon's side length is approximately 0.517, yielding a perimeter of 6.212, which gives us π ≈ 3.106. We're gradually approaching the accurate value! Indeed, by iterating this bisection method, one can achieve infinite precision, though computational complexity increases with each iteration. The mathematician Ludolph Van Ceulen, who lived in the 16th century, famously calculated π to 35 decimal places, employing a polygon with 2n sides—a considerable investment of time and effort for just a handful of digits.

Isaac Newton's Contribution
In the 1660s, a young Isaac Newton began exploring binomials and their powers, particularly the binomial expression (1+x)ⁿ. He recognized that the coefficients in its expansion correspond to the digits in Pascal's triangle. For instance, (1+x)² expands to 1 + 2x + x², representing the second row of the triangle (where rows are numbered starting from 0). Each row of the triangle is formed by summing adjacent numbers from the row above. The third row (1,3,3,1) is derived from the second as (1,1+2,2+1,1). While these properties were known for centuries, no one had previously applied this construction beyond positive integers. Newton's insight lay in demonstrating that the relationship between the binomial and Pascal’s triangle holds true even for negative integers and rational numbers, revolutionizing mathematics by enabling the calculation of roots through rational numbers.

Connecting Roots and Circles
How do binomials relate to π? Newton began with the equation of a unit circle: x² + y² = 1. Solving for y yields the upper half of the circle: y = (1-x²)½. This equation resembles the binomials we've examined. By substituting -x² for x and using ½ as the exponent, we can calculate y-values for points on the circumference using the binomial expansion. The key question remains: how do we extract π from this? Fortunately for Newton, he had just developed calculus.
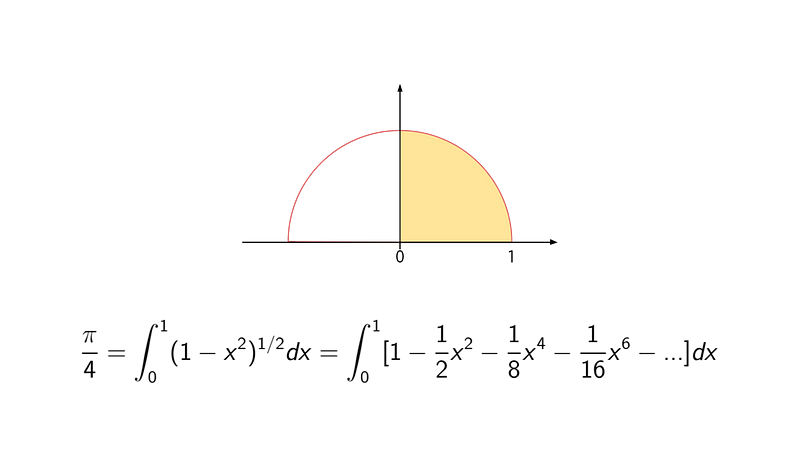
Integration of the Binomial Expansion
Now that we have an equation for the upper points of a unit circle (a circle with a radius of 1), we can simplify our focus to just the upper half (the quarter of the circumference between x=0 and x=1). We know that the area of this quarter is π/4. By summing the y-values derived from the upper circle equation for x-values between 0 and 1, we can estimate this area. Using a sufficient number of x-values will eventually lead us to π/4. This process embodies integration, where we partition the x-axis into infinitesimally small segments (dx) and sum the function's values across these intervals. Newton employed integrals to determine the area, substituting the actual circle formula with the binomial expansion for simplicity. This made the calculations straightforward, as the integral of a summation equals the summation of the individual integrals. Moreover, integrating constants and powers is quite elementary. Notably, the binomial expansion allows for selecting the desired accuracy level of the result. To achieve the precision of Ceulen's 35 decimals, we require only about 50 terms in the expansion.
This article delved into the remarkable tale of π's calculation and how mathematicians innovatively approached the challenge to achieve greater precision with less effort. If you found this article engaging, consider subscribing to Medium for unlimited access to its rich content. Enjoy!