Chapter 1: Understanding Manifolds

In the realm of general relativity, we deal with smooth shapes that resemble flat surfaces in small local areas. These smooth structures are referred to as manifolds, a fundamental and intuitive concept in differential geometry. The remarkable aspect of manifolds is that they allow us to establish coherent coordinate systems. For instance, by selecting a small segment of a manifold, we can create a coordinate system akin to those used in three-dimensional space.

The above illustration depicts small regions that help define a ‘coordinate’ system on the manifold. The arrows in the diagram indicate how these regions correspond to two-dimensional axes. Additionally, smooth functions at the intersections of these regions enable us to transition from one coordinate system to another.

Before we delve deeper, let me provide a more technical definition of a manifold for those interested in the specifics. A manifold is a space where, at every point, there exists a neighborhood that can be smoothly mapped to a subset of R^n. Since we have a solid grasp of spaces like R³ or higher dimensions, we can define intriguing objects at any point within the manifold, as the local neighborhood is well understood. The most significant phenomena, such as curvature and tangent vectors, are defined in relation to a single point.

One key concept we can define is tangent vectors. These vectors represent the rate of change of a function in a specific direction on a manifold. Visually, they appear as arrows that glide tangentially along the manifold at a point. Tangent vectors embody the idea of velocity in general relativity. The collection of tangent vectors at a specific point constitutes a tangent space.

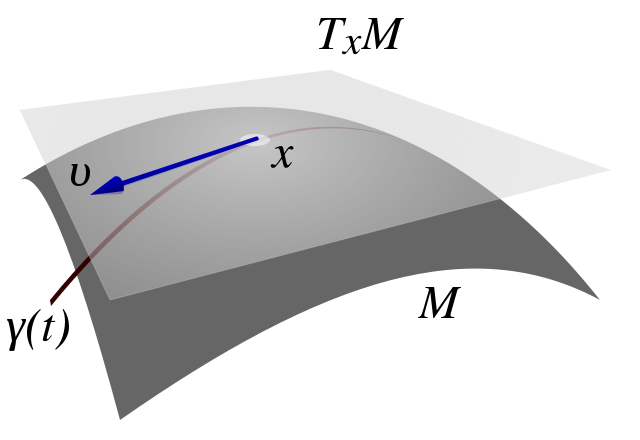
We can perform operations such as addition, subtraction, and scaling on tangent vectors at a single point on the manifold, similar to manipulations of vectors in high school geometry. Consequently, the set of tangent vectors at a point forms a vector space, which is a crucial concept in mathematics, as we have a comprehensive understanding of linear functions within vector spaces.

Section 1.1: The Concept of Fibrations

So far, we have only discussed the tangent space at an individual point on the manifold. However, we must also consider how to establish connections between different tangent spaces across the manifold. How do the mathematics and physics of tangent spaces vary as we navigate the manifold? To address these questions, we need to conceptualize how vector spaces ‘roll’ over the manifold. Essentially, we aim to formalize the entirety of tangent spaces associated with each point on the manifold.

To achieve this, we must employ mathematical principles from geometry and topology. We need to understand how to create new structures from existing objects. This article will elaborate on the concepts of fibre bundles and fibrations, providing relevant examples. In topology, a fibration involves using one space as a ‘parameter space’ for multiple other spaces. For instance, imagine a sphere with a tangent plane attached to each point, creating a scenario where locally, every point appears as a ‘product space’.

Section 1.2: Fundamental Concepts in Topology

To define a fibre bundle, we must grasp some essential topological concepts. A topological space is a specific type of mathematical structure with a formal definition. It is characterized by the notion of closeness and neighborhoods, which are defined through mathematical objects known as open sets. Formally, a topological space comprises an underlying space combined with a designated collection of open sets that are subsets of this space. Thus, consider a topological space as a derived object from any underlying space.

We can denote a topological space as a pair — the space itself, labeled X, along with a collection of subsets. For example, a topological space can be expressed as the double T=(X, ?), where X represents the underlying space and ? signifies the specific collection of subsets. A topological space must satisfy several axioms to qualify as such. Firstly, both the empty set and the set X must be included as open sets. Secondly, any union of open sets must also be an open set. Lastly, the finite intersection of open sets must remain an open set.

Mathematicians often engage in constructing complex topological spaces from simpler ones. One of the initial exercises is to ‘multiply’ topological spaces together. A product topology refers to a topological space induced by combining two topological spaces. For example, merging two copies of the line [0, 1] results in the formation of a square.

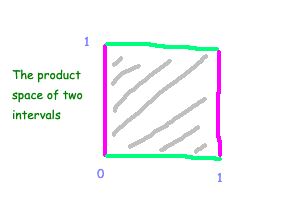
More formally, the product topology is the smallest topology ensuring the projection function remains continuous (in the topological sense). For instance, let X¹ and X² represent two real lines, each with topologies induced by the standard Euclidean metric. We can define two projections, denoted as p¹ and p², which map the two lines onto a single line.

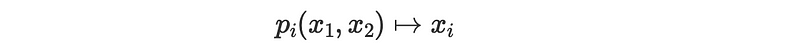
This projection is evidently continuous concerning the topology derived from the two-dimensional Euclidean metric; thus, the product topology is precisely this.

Chapter 2: Fibre Bundles Explained

A fibre bundle constitutes a ‘large’ space that can be projected down into a smaller space known as the base space. The ‘projection’ function is analogous to how a projector compresses a three-dimensional image into two dimensions. Imagine this process as condensing a three-dimensional hologram onto a two-dimensional surface. The projection map is typically represented by the Greek letter ?.

The inverse function of this projection must map any neighborhood back to a product space locally. This means that if we take a section of the compressed space and attempt to reconstruct the larger space, this larger space should resemble a ‘product’ of two spaces. Picture a tightly compressed slinky that expands out; the two-dimensional base space resembles a circle, while the inverse corresponds to a cylinder. Formally, a fibre bundle consists of a set of topological spaces E, B, F, coupled with a continuous surjection ?, adhering to specific conditions.

Firstly, the map ?: E?B must be a continuous surjection. A surjection is a mapping wherein every element in the base space B corresponds to an element in E that maps to it. Secondly, for any neighborhood in the base space, there exists a continuous, invertible map that provides a homeomorphism from the inverse of the projection to a product space B×F, encompassing the base space and fibre. This means that for any b?B, a point in our base space, we can identify a local neighborhood b?Ub, where we can find the homeomorphism.

Finally, certain compatibility conditions must be satisfied by the inverse map. For instance, the homeomorphism that identifies B×F, when composed with a projection map onto the first coordinate, should match the outcome of merely applying ? itself.

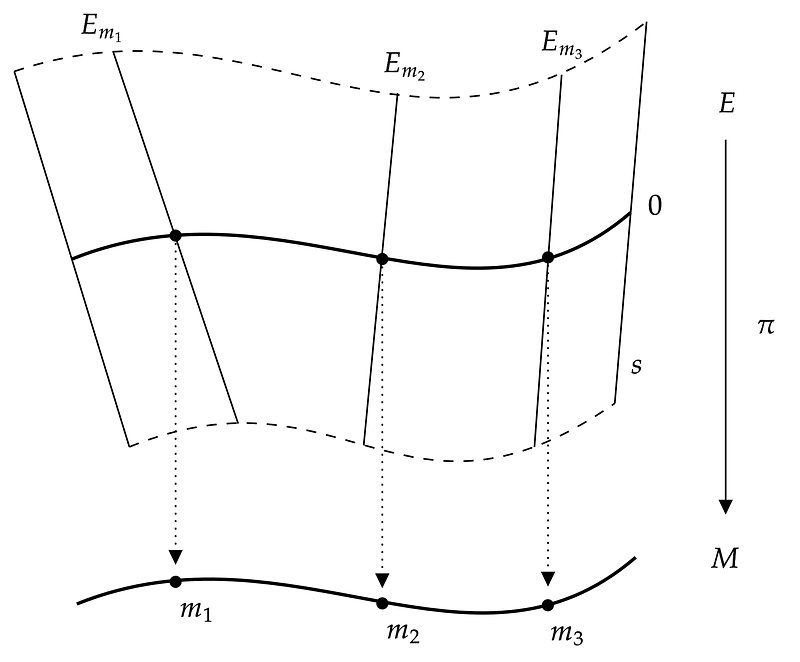
The diagram above effectively demonstrates this concept. The ‘large space’ is represented by space E, which appears as a two-dimensional strip. The base space is the single line M onto which the strip is projected. For any segment of line M, we can trace it back to the two-dimensional strip in space E. These small strips are referred to as fibres, and since the slices within this two-dimensional strip resemble a product space, we have a fibre bundle.

The intriguing aspect is that this condition is less stringent than requiring the global space to be a product space. For example, certain ‘non-trivial’ fibre bundles cannot be represented globally as product spaces, yet locally, we can expand neighborhoods of the base space into product spaces. Two crucial types of fibre bundles are tangent bundles and frame bundles.

A tangent bundle is a bundle where the typical fibre at any given point is the vector space R^n, for an n-dimensional manifold. This type of bundle serves as the foundation for Einstein’s theory of general relativity and describes the dynamics of tangent spaces traversing along manifolds. More examples will be provided in a future article!